第二章: 构筑抽象数据
2.1 介绍
在第一章我们集中关注计算过程, 以及函数对程序设计的作用与影响. 我们已经见识过如何使用原始数据(numbers)以及原始操作符(算术), 如何通过组合和控制来组成复合函数, 以及通过给计算过程赋予名称来创建函数抽抽象. 我们也看到高阶函数通过允许我们自行控制, 从而推理出一般计算方法来增强我们的语言的力量. 这就是编程的本质.
这一章主要关注数据. 我们在这里探讨的技术允许我们表达以及操作许多不同领域的信息. 由于因特网的爆炸性增长, 提供给我们大量在线且免费的结构化信息, 并且可以在大范围不同问题上进行计算. 有效使用內建的以及用户定义的数据类型是数据处理程序的根本.
2.1.1 基本数据类型
每一种数据在Python中都有一个类属, 这个类属决定了这个值是什么类型. 共享的数据同时具有共享的行为. 例如, 整数1以及2都是int类的实例. 这两个值能够进行类似的处理. 例如, 它们都可以被另外一个整数加或者减. 內建的type函数允许我们检查任何数值的类型.
|
|
我们目前使用的数值知识少量Python语言的內建_本地_数据类型. 本地数据类型具有以下属性:
- 有对原生类型的值进行定义的表达式, 叫做常量
- 有对原生类型的值进行操作的內建函数以及操作符
int类是用来表示整数的原生数据类型. 整型常量(相邻数字序列)表达为int值, 以及数学运算符来操作这些值.
|
|
Python包含有三种本地数据类型: 整型(int), 实数(float), 以及复数(complex).
|
|
Floats: 名字float来源于Python以及许多其他的程序语言实数的表示方式是以: “浮点(floating point)“来表示的. 至于数字是如何表示的这些细节不在我们这一节的讨论范围之内, 而一些int以及float对象的高级差异需要重点了解. 尤其是, int对象能够准确地表示整数, 对其大小没有任何近似以及限制. 另一方面, float对象能够表示较宽范围内的分数, 但不是所有的数字都能够准确表示, 同时它们还具有最小值以及最大值. 因此, float数值应该被视为实际值的近似值来对待. 这些近似值只具有有限的精度. 合并浮点数会导致一些精度错误; 如果不用近似值的话下面的表达式计算后应该会等于7:
|
|
虽然上面是int的组合, 用一个int除以另一个会得到一个float的值: 一个被截断了的近似值, 也就是两个整数相除的实际比率.
|
|
当我们进行相等性测试的时候就会出现近似值的问题.
|
|
这些int类型与float类型之间的微妙不同, 对程序的编写具有广泛的影响, 因此它们的细节程序员必须要铭记在心. 幸运的是, 只有少量的本地数据类型, 限制了精通编程语言所需要的记忆量. 此外, 这些相同的细节在许多编程语言中也是一致的. 由社区准则强制执行, 如: IEEE 754 floating point standard
非数字类型. 数值能够代表许多其他类型的数据, 例如声音, 图像, 地点, 网址, 网络连接等等. 少量是通过本地数据类型来表示的, 例如代表真(True)和假(False)的布尔(bool)类型. 大多数值的类型都需要程序员来使用本章中研究的组合和抽象手段来进行定义.
接下来的部分将介绍更多Python的本地数据类型, 侧重于它们在创建有用的数据抽象中所起到的作用. 那些对于更加深入的细节感兴趣的人可以阅读一下深入Python3这本书的本地数据类型这一章,写出了所有Python的本地数据类型的实用概述以及如何对它们进行操作, 包括大量的用法例子以及练习提示.
2.2 数据抽象
当我们考虑世界上的广泛的事物的时候, 我们会想要将它在我们的程序中表现出来, 我们会发现它们大多数都具有复合结构. 例如, 一个地理位置有经度以及纬度坐标. 为了表示位置, 我们会想让我们的程序语言有能力将经度和纬度合在一起以形成一对, 作为一个我们的程序能够操作的一个单一的概念单元, 但是它也具有两个部分可以进行单独考虑.
使用复合数据能够让我们提升程序的模块性, 如果我们能够将地理位置作为一个整体来进行操作, 然后我们就可以对程序使用位置进行计算中是如何对这些地理位置进行表示的细节进行屏蔽. 一般的隔离程序各个部分的技术, 都是处理数据是如何被表示, 以及处理数据是如何被操作的强大的设计方法, 这方法称为数据抽象. 数据抽象让程序更容易被设计, 维护, 以及修改
数据抽象在性质上跟函数抽象那一章相似. 当我们创建一个函数抽象, 函数是如何实现的细节能够被压制, 以及特定的函数本身能够被任何其他的具有相同整体行为的函数进行替换. 换句话说, 我们可以实现一个抽象来将函数使用的方式与函数如何实现的细节上进行分离. 类似地, 数据抽象对复合数据的使用方式与如何构造的细节进行了隔离.
数据抽象的基本思想是结构化程序, 以便于它们对抽象数据进行操作. 也就是说, 我们的程序应该以尽可能少的以对数据进行假设的方式来使用数据. 同时, 数据的具体表现应该定义为程序的一个独立的部分.
程序的这两个部分, 对数据抽象进行操作的部分以及定义具体表示的部分, 通过一组小的函数进行连接, 这些函数根据具体表示实现抽象数据. 为了说明这种技术, 我们需要考虑如何设计一套函数来操作有理数.
2.2.1 例子: 有理数
一个有理数就是整数的比率, 有理数是构成实数的重要子类. 一个有理数如1/3或者17/29通常写作:
<numerator>/<denominator>
而<numerator>以及<denominator>都是整数的占位符. 这些部分都需要用来准确地表征有理数的值. 实际上整数相除得到一个浮点数的近似值, 失去了整数的精确度.
|
|
然而, 我们可以通过将分子和分母组合在一起来为有理数创建一个精确的表示.
我们从使用函数的抽象中可以知道, 我们可以在程序的某些部分实现之前开始进行编程. 让我们假设我们已经有办法从一个分子以及一个分母中构造一个有理数开始. 我们还假设, 给定一个有理数, 我们有方法选定它的分子和分母的部分. 让我们进一步假设构造器以及选择器可具有一下的三个功能:
- **rational(n, d)**以分子为n分母为d的形式返回一个有理数
- **numer(x)**返回有理数中的分子x
- **denom(x)**返回有理数中的分母x
在这里我们使用程序设计中的强大策略: 祈愿思维. 我们还没有讲述一个有理数是如何表示的, 或者函数number, denom, 以及rational应该怎么实现. 即使这样, 如果我们定义了这三个函数, 我们可以对有理数进行加, 乘, 打印, 以及测试相等性等操作:
|
|
现在我们具有定义在选择器函数number以及denom和构造器函数rational之上的操作函数, 但是我们还没有定义这些选择器函数以及构造器函数. 我们需要一种方法来将分子和分母进行粘合, 形成一个复合值.
2.2.2 一对
为了让我们实现正确等级的数据抽象, Python提供了一种复合数据结构叫做list, 能够通过将表达式放到方括号内并用逗号分隔开来构造, 这种表达式就叫做列表字面量.
|
|
列表中的元素可以用两种方式来进行访问, 第一种方式是通过我们熟悉的多重分配的方法, 通过对list对象中的元素进行解包然后绑定每一个元素到不同的名字.
|
|
第二个访问方法是通过list的元素选择运算符, 也通过方括号来进行表达. 不像列表字面量, 一个方括号表达式直接跟在另一个表达式后面不以生成列表值来运行, 而是在前面的表达式中选择一个元素.
|
|
在Python中的列表(以及大多数其他的编程语言)是以0索引作为开始的, 这意味着索引0选定第一个元素, 索引1选定第二个, 等等. 一个支持这个索引惯例的直觉是索引代表一个元素偏离列表开始位置有多远.
跟元素选择操作符相等的函数叫做getitem, 它也用索引0作为开始位置来对列表对象进行选取.
|
|
两个元素的列表不是表示一对的唯一方法, 任何将两个值捆绑到一块的方法都可以认为是一对. 只是列表是一种常用的方法. 列表也可以容纳超过两个对象, 正如我们本章接下来要进行讨论的.
表示有理数. 现在我们能够将有理数表示为一对整数的组合: 一个分子和一个分母.
|
|
结合早先我们定义的算术运算, 我们可以用我们已经定义好的函数来操作有理数.
|
|
像上面例子显示的那样, 我们的有理数的实现不会将有理数减少到最低项. 我们可以通过改变rational函数的实现来修复这个缺陷. 如果我们有一个函数来计算两个整数的最大公分母, 我们就可以在构建有理数对时用它来将分子和分母减少为最底项. 跟许多有用的工具一样, 在Python的库中已经有这样的一个函数了.
|
|
整除运算符, //, 表示整除, 也就是对相除的结果将向下舍入小数部分. 由于我们已经知道g能够完全整除n以及d, 整除在这种情况下是精确的. 这个rational函数的合理地进行了修正保证了有理数以最低项来表示.
|
|
这种改进是通过改进构造函数而不用改变其他函数(即实现实际运算的函数)来完成的.
2.2.3 抽象屏障
在继续(介绍)更多的组合数据和数据抽象的例子之前, 让我们思考一下有理数例子提出的一些问题. 我们根据构造函数rational和选择器numer, denom定义操作. 一般来说, 数据抽象的基础思想是识别一组基础操作, 根据这些操作来表达某种类型的值的所有操作, 然后只使用这些操作来处理数据. 通过限制这些操作的使用方式, 将会更容易改变抽象数据的表示而不用修改程序的行为.
对于有理数, 程序的不同部分使用不同的操作来操纵有理数, 如下表所述:
| Parts of the program that… | Treat rational as… | Using only… |
|---|---|---|
| Use rational numbers to perform computation | whole data values | add_rational, mul_rational, rationals_are_equal, print_rational |
| Create rationals or implement rational operations | numerators and denominators | rational, numer, denom |
| Implement selectors and constructor for rationals | two-element lists | list literals and element selection |
| 程序的每个部分… | 将有理数当做… | 只用作 |
|---|---|---|
| 用有理数来执行计算 | 整个数值 | add_rational, mul_rational, rationals_are_equal, print_rational |
| 创建有理数或操作有理数 | 分子以及分母 | rational, numer, denom |
| 实现有理数的构造器以及选择器 | 两个元素的列表 | 列表字面量以及元素选择 |
在上面的每一层, 最后一列的函数实现了一个抽象屏障. 这些函数通过更低层次的抽象来实现来被更高层的函数调用.
违反一个抽象屏障的情况发生在每当可以在较高级别函数中使用程序的一部分时, 却使用较低级别的函数来实现. 举个例子, 一个计算有理数平方的函数最好是根据mul_rational来实现, 而无需对有理数的实现进行任何假设.
|
|
直接涉及到分子以及分母会违反一层抽象屏障.
|
|
假设有理数用两个元素的列表表示会违反两层抽象屏障.
|
|
抽象屏障让程序更容易管理与修改. 越少函数依赖于特定的表示, 当想改变其中一个的表示的时候就需要越少的改动. 所有的这些square_rational的实现都具有正确的行为, 但是只有第一个对于未知的变化是健壮的. square_rational函数即使在我们修改有理数的表示的时候也不需要更新. 相比之下, square_rational_violating_once每当选择器或者构造器的特征改变的时候都需要进行修改, 而square_rational_violating_twice则在有理数的实现有任何改变时都需要进行更新.
2.2.4 数据的属性
抽象屏障能够塑造我们思考数据的方式. 对有理数进行有效的表示是不限于任何特定的实现的(如具有两个元素的列表); 它是rational函数返回的一个值, 这个值能够输入到numer以及denom当中. 除此之外, 必需维持构造器跟选择器之间恰当的关系. 也就是说, 如果我们从整数n跟d中构造一个有理数x, 应该得到一种情况是numer(x)/denom(x)等于n/d.
一般来说, 我们可以用选择器函数以及构造器函数集合与一些行为条件一起来表示抽象数据. 只要这些行为条件满足(例如上面的除法属性), 选择器以及构造器函数构成了一种数据的有效表示. 在抽象屏障之下的细节可能会有更改, 但是如果行为没有改变, 那数据抽象依然是有效的, 然后任何使用这些数据抽象编写的程序依然是正确的.
这一观点能够进行广泛地应用, 包括我们用于实现有理数的数据对. 我们从没有说过什么是数据对, 只有语言提供的创建以及操作两个元素的列表方法. 我们需要实现的数据对的行为是它能将两个值黏合在一起. 而行为条件,
- 如果一个数据对p由值x跟y构造, 那么select(p, 0)返回x, select(p, 1)返回y.
我们实际上不需要用列表类型来创建数据对, 作为替代, 我们可以实现两个函数pair以及select来满足这个描述, 就像两个元素的列表一样.
|
|
有了这个实现, 我们可以创建并操作数据对.
|
|
这种高阶函数的使用方式能够跟我们对于数据是什么这种直观的概念进行对应. 然而, 这些函数足够表示我们程序中用到的数据对. 函数足以表示复合数据.
用函数展示数据对的意思不代表Python就是以这种方式来运行的(处于效率的原因, 列表的实现更加的直观)但是它能以这种方式运行. 函数型的表示虽然模糊, 但它完全具有表示数据对的能力, 因为它满足数据对唯一需要满足的条件. 数据抽象的实践允许我们轻易地在各种表示中进行切换.
2.3 序列
序列就是一个值的有序集合. 序列在计算机科学中是强大的, 基本的抽象. 序列不是某个特定的內建类型的实例或者抽象数据表示, 而是在一些不同类型的数据之间共享行为的集合. 也就是说, 有许多种类型的序列. 但是它们都共享共同的行为. 尤其是,
长度. 一个序列具有有限的长度. 一个空序列的长度是0.
元素选择. 一个序列的对于任何小于它长度的非负整数的索引值都对应它的一个元素, 第一个元素从0开始.
Python包含的一些本地数据类型就是序列, 最重要的莫过于列表了.
2.3.1 列表
一个列表就是一个具有任意长度的序列. 列表具有一大套內建行为, 以及表示这些行为的特殊语法. 我们已经见识过列表字面量了, 也就是用来运算生成列表实例那个, 以及元素选择表达式, 即用来获取列表中的值的语法. 內建的len函数用于返回一个序列的长度. 下面, digits是一个具有四个元素的列表. 索引为3的元素值是8.
|
|
另外, 列表可以加在一起, 以及与一个整数相乘. 对于序列来说, 加法以及乘法不会添加或者乘里面的元素, 而是复制序列本身并将它们合并在一起. 也就是说, 在operator模块下的add函数(以及符号+)返回的是添加的参数级联后生成的一个列表. 而在operator中的mul函数(以及*号)能够传入一个列表以及一个整数然后返回另一个列表, 这个列表是由k次重复的源列表组成的.
|
|
任意的值都可以包含在列表中, 包括其他的列表. 为了选择到包括在列表里面的列表这样深层次嵌套的元素可以多次应用列表元素选择语法.
|
|
2.3.2 序列迭代
在很多情况下, 我们会想要对序列的元素进行迭代然后反过来对每个元素执行一些计算. 这种模式是如此的常见以至于Python有一个额外的控制语句来处理顺序的数据: for语句.
想一下计算一个值在序列中出现的次数这样的一个问题, 我们可以实现一个函数用while循环来进行计数.
|
|
Python的for语句能够简化这个函数体通过直接对元素值进行迭代而根本不需要引入名称index.
|
|
for语句由单个子句组成, 形式如下:
for <name> in <expression>:
<suite>
一个for语句会按照以下的步骤执行:
- 计算头部表达式
<expression>, 必须返回一个可迭代的值. - 遍历该可迭代值中的每一个元素, 是为了:
- 将这个元素值当前域的中的
<name>进行绑定 - 执行
<suite>
- 将这个元素值当前域的中的
这个执行过程引用的是可迭代的值, 列表是序列的一种, 而序列是一种可迭代的值. 它们的元素按照它们原有的顺序被考虑. Python包括其他的可迭代的值, 但是目前我们会专注于序列; 术语"可迭代"的一般定义出现在第四章的迭代器部分.
这个计算过程的一个重要的意义是<name>会在for语句运行后绑定到序列中的最后一个元素. for循环引入了另外一种可以让运行环境随语句执行而更新的方式.
序列解包. 在程序中的常见模式是有一个以序列为元素的序列, 但元素都是固定长度的. 一个for语句可能会包含有多个名称在它的头部用来对序列中的每一个序列元素"解包"到各自对应的名称上. 例如, 可能会有一个以包含两个元素的序列为元素的序列:
|
|
然后希望从中找到这些序列对中两个数字是相等的序列对
|
|
下面的for语句在它的头部有两个变量名x和y, 这两个变量名会分别跟序列对的第一和第二个元素进行绑定:
|
|
这种将多个名称以固定长度的顺序绑定到多个值的模式称为序列解包; 这跟我们在赋值语句中看到的绑定多个名称到多个值的模式是一样的.
范围. 一个range类型是Python中另一个內建的序列类型, 它代表了一个整数的区间. 区间由range来创造, 需要两个整数作为参数: 第一个数字和一个超出所需范围内的最后一个数字.
|
|
调用list构造器计算出在一个在范围内的与范围相符的列表, 因此可以很容易地检查里面的元素.
|
|
如果只给定一个参数, 这被解析为构建一个从零开始到超出所需范围内的最后一个数字的区间.
|
|
区间通常出现在for表达式的头部来指定<suite>部位应该执行的次数: 有一个共同的约定是如果在for的头部写入的名称在<suite>中没有用到的话就用单个下划线作为名称:
|
|
下划线对于解释器环境而言只是另外的一个名称, 但是它在程序员之间却是具有常规的意义, 那就是表明这个名称不会现在在之后的任何表达式中.
2.3.3 序列处理
序列是一种如此常见的用于组成复合数据的形式以至于整个程序通常都围绕这个单一抽象来进行组织. 模块化组件同时以序列作为输入和输出能够对数据处理过程进行混合以及匹配. 复杂组件能够通过将序列处理操作连接在一起形成管道来进行定义, 而每个处理都是简单和集中的.
列表推导. 很多的序列处理操作能够通过为序列中的每个元素计算一个固定的表达式然后收集结果的值到一个结果序列中来表示. 在Python中, 一个列表推导式是一个执行这样的计算的表达式:
|
|
上面的for关键词不是for语句的一部分, 而是列表表达式的一部分因为它包含在方括号里面. 而子表达式 x+1 是将x顺序绑定到每一个odds中的元素来进行运算, 然后收集每次运算的结果到列表中.
另一个常见的列表推导操作是去选择一个满足某些结果的子集. 列表推导能够表达这种模式, 例如选择所有odds中的能够整除25的元素:
|
|
列表推导的一般形式是:
[<map expression> for <name> in <sequence expression> if <filter expression>]
为了运算一个列表推导, Python会计算<sequence expression>, 这个表达式必须要返回一个可迭代值. 然后, 对每个元素按照顺序, 将元素的值与<name>进行绑定, 接着运算过滤表达式, 然后如果过滤结果返回真值, map expression(映射表达式)将会执行, 最后结果会被收集到一个列表中.
聚合. 第三个序列处理的一般模式是将一个序列中所有的值聚合到单一的一个值中. 內建函数sum, min, 以及max所有都是聚合函数的例子.
通过结合这些对每个元素进行运算, 选择元素的子集, 以及聚集元素的模式, 我们可以使用序列处理方法来解决问题.
一个完备正整数指的就是一个等于它的除数的总和. n的除数是小于n且能均分n的正整数. 可以通过列表推导来运算从而列出这些n的除数
|
|
使用divisors函数, 我们可以用其他的列表推导来计算出从1到1000的所有的完备数. (1通常也被认为是完备数, 但是它不符合我们对divisors的定义)
|
|
我们可以复用我们定义的divisors来解决另外的问题, 找出一个具有固定面积以及整数长度边长的长方形的最小周长. 长方形的面积等于它的高乘以宽. 而且, 给定面积以及高, 我们可以计算出宽. 我们可以肯定地说, 长和宽都能均分面积的话, 就可以保证边长都是整数.
|
|
长方形的周长等于它边长的总和
|
|
具有整数边长的长方形的高必须是它面积的除数. 我们可以通过考虑它所有的高来计算最小周长.
|
|
高阶函数
我们在序列处理中观察到的一般模式可以用高阶函数来进行表示. 首先, 为序列中的每个元素运行一个表达式可以通过对每一个元素应用函数来来表示.
|
|
通过对每一个元素应用的函数表达式然后仅选择能使表达式结果为真的元素.
|
|
最后, 许多形式的聚合可以表示为反复应用一个带有两个参数的函数, 分别是进行reduced后的值, 以及顺序应用的每一个元素.
|
|
例如, reduce可以用来将序列中的所有元素乘到一起. 使用mul替代reduce_fn, 1替代initial, reduce可以用来将序列中的数都乘到一起.
|
|
我们也可以用这些高阶函数来找寻完备数
|
|
常规名称
在计算机科学的社群中, apply_to_all一般叫做map, keep_if一般叫做filter. 在Python中, 內建的map以及filter是这些方法的泛化, 且并不返回列表对象. 这些方法会在第四章来进行讨论. 上面的定义相当于用列表构造器到处理內建的map以及filter调用后所返回结果.
|
|
reduce函数构建在Python的标准库的functools模块中. 在这个版本中, initial参数是可选的.
|
|
在Python程序中, 直接使用列表推导是比使用高阶函数更一般的模式, 但两者在列表处理中都是广泛使用的方法.
2.3.4 序列抽象
我们已经介绍了两种满足序列抽象的本地数据类型: 列表和区间(lists and ranges). 两者都满足这部分开始所设的条件: 长度以及元素选择. Python包含了额外的两个序列类型的行为用来进行序列抽象的拓展.
成员. 一个值能够就是否是一个序列的成员来进行测试. Python有两个操作符in以及not in其计算的结果是True或者False取决于元素是否出现在序列中.
|
|
切片. 序列都包含更小的序列. 一个序列的切片是原有序列的任何一个连续片段, 由一对整数来指定. 就像range构造函数一样, 第一个整数指定了切片的起始下标, 然后第二个整数指定了超过结束下标的数.
在Python中, 序列切片的表达式跟元素选择类似, 用方括号包裹. 一个冒号分割起始以及结束索引. 任何省略的边界都被认定为一个极值: 0是开始下标的极值, 而序列的长度则是结束下标的极值.
|
|
切片也可以用于树的分支上. 例如, 我们可能想要对一些树的分支数进行限制. 一个共同的树转型通过将原始树进行分组组合并调整分支得出的一个二叉树叫做二值化计算.
|
|
对Python序列抽象中的这些额外行为进行枚举给我们一个机会来反映一个一般有用的数据抽象的组成. 抽象的丰富性(也就是说它包含的行为有多少)是有意义的. 对用户来说, 一个抽象的, 额外的行为可能很有帮助. 另一方面, 用一个新类型来满足对丰富抽象性的要求可能很具挑战性. 另一个丰富抽象性的负面后果是它们可能需要用户用更长的时间来学习.
序列具有丰富的抽象性因为因为它们在计算机中是如此的无所不在, 以至于需要学习一些复杂的行为是合理的, 一般来说, 大多数用户定义的抽象应该尽可能保持简单.
深入阅读. 切片符号收录了各种各样的特殊例子, 例如负的起始值, 结束值以及步进大小. 一个完整的描述出现在Dive Into Python 3的子节中叫做切片列表. 在这节章中, 我们只会使用到上面提及的基础特性.
2.3.5 字符串
文本值在计算机科学中可能是比数字要更一般的存在. 作为例子, Python程序的都是以文本进行编写以及存储. Python中作为文本的本地数据类型被叫做字符串, 而对应的构造器就是str.
在Python中关于字符串的表现, 表达以及操作有很多的细节. 字符串是另一个丰富抽象的例子, 一个需要程序员承诺牢固地掌握的部分. 此部分会用作对基本字符串行为的简明介绍.
字符串字面表达式通过用单引号或者双引号作为记号来包围可以表达任意的文本.
|
|
我们已经在代码中见识过字符串了, 如docstring, print函数的调用中, 以及在assert语句中的错误消息.
字符串满足我们在本节最开始介绍的序列的两个基本条件: 它们具有长度以及支持元素选择.
|
|
属于字符串本身也是字符串, 只不过它们只有一个字符. 字符是字母表的任意单个字符, 标点符号, 或者其他符号. 不像许多其他的编程语言, Python没有分开字符类型; 任何文本都是字符串, 单一一个字符代表一个长度为一的字符串.
就像列表, 字符串也可以用加法或者乘法来进行结合.
|
|
成员. 字符串的行为发散自Python中的其他序列类型. 字符串抽象不符合我们描述的列表以及区间那样的全序列抽象, 尤其是, 当成员运算符in应用到字符串时, 却会有跟应用到序列上完全不同的行为表现. 它匹配的是子字符串而不是元素.
|
|
多行文本. 字符串并不限制只有一行. 三重引号划定了字符串文本可以跨越多行的范围. 我们已经对docstring广泛使用这个三重引号了.
|
|
在上面打印出来的结果中, 那个\n(发音是"backlash en”)是一个单元素, 用来代表一个新行. 即使它是用两个字符来表示的(backslash 以及 n), 它在长度以及元素选择上依然被认为是单个字符.
字符串强制转换. 一个字符串能够从Python的任何对象中通过调用str构造器函数以一个对象作为它的参数来构建. 这个字符串的特性对于从各种类型的对象中构造描述性的字符串是十分有用的.
|
|
深入阅读. 编码文本在计算机中是一个复杂的主题. 在这一章中, 我们会抽象出字符串是如何表示的细节. 然而, 对许多应用来说, 字符串是如何被计算机编码的特定细节是是必要的知识. 在The strings chapter of Dive Into Python3中提供了字符编码以及Unicode的描述
2.3.6 树
我们有将一个列表作为另一个列表内的元素来使用的能力, 在我们的编程语言中提供了一种新的组合手段. 这种能力叫做数据类型的闭包属性. 一般来说, 如果组合数据的方法组合出来的结果本身可以用于这个组合方法就说这个组合方法具有闭包属性. 闭包是任何组合手段的关键源泉, 因为它允许我们去创建分层的结构–由部件组成的结构, 而这个部件本身又是由其他部件构成的等等.
我们可以在环境图中通过块以及指针符号对列表进行可视化, 一个列表描述为一系列包含列表中元素的相邻块. 原始值如数字, 字符串, 布尔值, 以及None值会出现在元素块中, 合成的数据, 如函数值, 以及其他列表, 会用一个箭头来表示.
将一个列表嵌套到另一个列表中会引入复杂性. 树是基本的数据抽象, 用于加强如何对分层数据进行结构化以及操作的规律性.
一棵树有一个根值以及一系列的分支. 树的每一个分支都是一棵树. 一棵没有分支的树叫做叶子. 任何被包含在另一个树中的树都叫做棵树树的子树(就像一个分支的分支). 而一棵树的一棵子树的根值又被称作这棵树的一个节点(或者节点值).
树的数据抽象由一个构造器tree以及选择器root和branches组合而成. 我们由最简单的版本开始.
|
|
只有当树具有根值并且所有分支也是树时,才会形式一棵良好的树. is_tree函数是用在tree构造器中用来校验是否所有的分支都形成良好.
|
|
is_leaf函数用来检查一棵树是否有分支.
|
|
树能够用嵌套表达式来构建, 下面的树t有根值3以及两个分支.
|
|
树递归函数可以用来构造一棵树. 例如, 一棵n阶斐波那契树以n阶斐波那契数作为根值, 对于n > 1时, 两个分支也是斐波那契树. 一个斐波那契树演示了斐波那契数的树递归计算.
|
|
树递归函数也用于处理树. 例如, count_leaves函数用于统计树的树叶的量.
|
|
分区树. 树可以用来表示整数的划分形式. 一个用最大为m的数划分数n来组成的分区树是一棵二叉树(两个分支), 代表了计算时候的两个选择. 在非叶子分区树中:
- 左边的(下标为0)分支包含了至少使用一个m来划分n的所有方式
- 右边的(下标为1)分支包含了用
m-1部分来划分的分区树, 以及 - 根的值是m
分区树叶子的值表示了从树的根到叶的路径是否代表一个n的成功分区.
|
|
从一个分区树打印出分区是另外一个遍历树的树递归过程, 将每一个分区构造成一个列表. 不管是否能够触及True叶子, 分区树都会打印出来.
|
|
2.3.7 链接列表
目前为止, 我们只用了原生的数据类型来表示序列. 然而, 我们也可以开发一个不是Python原生的序列表示. 一个序列的常见表示法是由嵌套的成对数据来构成, 叫做列表. 下面的环境图例表示出一个由四个按顺序包含1, 2, 3和4的元素组成的链表.
一个链表是一个成对的数据, 包含了序列的第一个元素(在例子中是1)以及剩下的元素的序列(在例子中是2, 3, 4). 第二个元素也是一个链表. 剩下的最里面的链表只包含4, 其余部分是empty, 一个用于代表空链表的值.
链表具有递归结构: 链表的其余部分是一个链表或者empty值. 我们可以定义一个抽象数据表示来进行验证, 构造以及选择链表的某部分.
|
|
上面, link是一个构造器, first以及rest是用于代表已经链接的列表抽象数据的选择器. 链表的行为条件是像数据对, 它的构造器以及选择器是其反函数.
- 如果一个链表s是由第一个元素是f以及一个已经是链表的r组成, 那么
first(s)返回的是f,rest(s)返回的是r.
我们可以用构造器以及选择器来操纵链表.
|
|
我们实现的这种类型的抽象数据是数据对, 一个具有两个元素的列表值. 值得注意的是, 我们也可以通过函数来实现对数据, 同时我们也可以用任何对数据来实现链表, 因此我们可以只用函数来实现链表.
链表可以按顺序存储一系列的数据值, 但是我们还没有展示它满足序列抽象的那一部分. 使用我们定义的抽象数据表示, 我们可以实现序列的两个特征行为: 长度以及元素选择.
|
|
现在, 我们可以用这些函数来把链表当做序列来操作. (我们现在还不能用內建的len函数, 元素选择语法, 或者for语句, 但是很快就可以了)
|
|
下面的一系列环境图例演示了getitem_link的找寻链表中下标为1的第二个元素的迭代过程. 下面, 我们已经用Python原语来简化图表来定义链表four. 这种实现选择违反了抽象边界, 但是允许我们更容易检视这个例子的计算过程
首先, 函数getitem_link被调用, 创建了一个本地帧:
while头部的表达式计算得到true, 然后while的内部等式会被执行, 函数rest返回以2开头的子列表.
接下来, 局部名称s会更新成以原列表第二个元素为开头的子列表的引用. 运算while头部表达式现在会返回false值, 然后Python运算在返回语句之后的getitem_link的最后一行表达式.
最后的环境图例显示调用first的本地帧, 也就是含有绑定到同一个子列表的名称s. first函数选择值2然后返回, 也会从getitem_link中返回.
这个例子演示了一个列表计运算的一般模式, 迭代操作中的每一步都会不断得到原列表中较短的后缀. 这查找列表长度以及元素的增量处理过程需要一些时间来运算. Python的內建序列类型是用不同形式实现的, 这让计算序列长度或者检索它的元素都不会导致很大的计算成本. 这种表现的细节已经超出本文的范围.
递归操作. len_link以及getitem_link函数都是迭代的. 它们不断剥离每一层的嵌套数据对直到到达到达列表的最后(在len_link函数中)或者到达期望的元素(在getitem_link中).我们也可以用递归来实现长度以及元素选择.
|
|
这些递归实现跟随数据对组成的链直到到达列表的最后(在len_link_recursive中)或者到达期望的元素(在getitem_link_recursive中).
递归对于转换以及合并链表也是有用的.
|
|
递归构建. 链表在我们增量地构造序列的时候尤其有用, 这种情况经常在递归计算中出现.
第一章中的count_partitions函数通过树递归过程来计算整数n用最大为m的数来进行分割的总数. 通过序列我们也可以通过明确地使用相似的过程来枚举这些切分.
跟我们计算时一样, 我们用跟随问题的相同递归分析: 用最大为m的整数来划分n涉及到
- 使用最大为m的整数来划分n-m, 或者
- 使用最大为m-1的整数来划分n
对于基本情况, 我们发现用一个负整数或者用小于1的部分来划分0是不可能的, 因此0的划分数为空.
|
|
在递归情况下, 我们构建两个分区的子列表. 第一个用m, 因此我们在结果using_m中的每个元素前面加上m来构建with_m.
partitions的结果是高度嵌套的: 一个链接列表的链接列表, 并且每个链接列表被表示为作为列表值的嵌套对. 在join_link函数中用恰当的分隔符, 我们可以用人类可阅读的方式来展示出分区.
|
|
2.4 可变数据
我们已经见识过抽象对于帮助我们应对大型系统的复杂性上的重要性了. 有效的编程依赖于有组织的能够指导我们在制定程序的整体设计的规则. 尤其是, 我们需要很多策略来帮助我们构造模块化的大型系统, 这意味着它们会自然分裂成各个相关的部分且能够分头开发以及维护.
有一个强大的创建模块化程序的技术, 那就是合并可能随时间改变状态的数据, 通过这种方式, 单个数据对象可以表示独立于程序的其余部分演进的东西. 改变对象的行为可能会受到其历史的影响, 就像一个真实世界的实体一样. 为数据添加状态是面向对象编程范式的核心要素
2.4.1 对象隐喻
在本文开头, 我们要区分函数跟数据: 函数用于执行操作, 而数据则是在其上被操作. 当我们在我们的数据中包含函数的值的时候, 我们认识到数据也可以具有行为. 函数可以作为数据来操作, 也可以被调用来执行计算.
对象将数据值与行为进行组合. 对象代表信息, 同时也表现得像它们所代表的事物. 一个对象跟另一个对象互动的逻辑是跟编码这个对象的值捆绑在一起的. 当一个对象需要被打印出来时, 它知道如何用文本来表示自身, 如果一个对象是由部分组合而成的, 那么它知道如何按需显示这些部分. 对象(包含的)全都是信息以及(处理)过程, (它们)捆绑在一起来表示复杂事物的性质, 相互作用和行为.
对象的行为在Python中是通过专门的对象语法以及相关术语来实现的, 我们可以通过例子来进行介绍, 一个日期是一个对象.
|
|
名称date绑定到一个类上的. 正如我们看到的, 一个类代表一种值. 个别的日期就叫做这个类的实例. 实例能够通过使用表明这个实例的特征参数来调用类来构建.
|
|
当用原始数字构造tues之后, 它的行为表现得像日期一样, 例如, 将它跟其他的日期相减会返回一个时差, 我们可以打印出来.
|
|
对象具有属性, 是一个命名后的对象的一部分的值. 在Python中, 像很多其他的编程语言一样, 我们用点符号来指定一个对象的属性.
<expression> . <name>
上面, <expression>是一个对象, 然后<name>是一个对象属性的名称. 不我们至今为止考虑过的名称, 属性名对于点符号前面的对象实例来说是独特的.
|
|
对象通常也有方法, 也就是属性值为函数的属性. 隐含的意思是, 我们认为这个对象"知道"如何去执行这些方法. 通过实现, (对象)方法是一个用来从它们的参数以及它们的对象中计算结果的函数. 例如, tues有一个strftime方法(一个经典函数的名称, 意思是"字符串格式的时间”)接受一个参数用于指定如何显示日期(例如: %A表示这周的某一天应该完整地拼写出来).
|
|
计算strftime的返回值需要两个输入: 一个用于描述输出格式的字符串以及绑定在tues中的日期信息. 特定日期逻辑需要应用这个方法来返回结果. 我们从来没有说过2014年5月13号是星期二, 但是知道它对应的是工作日的一部分, 这就意味着它是一个日期. 通过将行为以及信息绑定到一起, 这个Python对象提供给我们一个可信的, 自足的日期抽象.
日期是一个对象, 而且数字, 符串吗, 列表以及区间等也全都是对象. 它们代表一个值, 而且还以符合它们表示的值的方式表现. 它们也有属性以及方法. 比如, 字符串具有一个数组方法用于方便文本处理.
|
|
实际上, 在Python中所有的值都是对象, 也就是说, 所有值都具有行为以及属性. 它们的行为就像它们所代表的值.
2.4.2 序列对象
原始內建的值的实例如数字是不可变的. 这个值在程序的执行过程中是不可变的. 而另一方面列表则是可变的.
可变对象用来代表随时间变化的值. 一个人是在今天到明天依然是同一个人, 尽管变得老了, 剪了头发, 或者以某种方式改变了. 同样地, 一个对象的属性可能会由于可变操作而改变了属性. 例如, 可以改变列表中的内容. 大多数改变通过调用执行列表对象内部的方法.
我们可以通过一个说明扑克牌历史的例子(大大简化)来介绍很多列表的修改操作. 在例子的注释中, 描述了每个方法调用的结果.
扑克牌是在中国发明的, 大约在9世纪. 较早的扑克牌只有三种花式, 分别跟钱的面额对应起来.
|
|
随着扑克牌传入欧洲(可能是通过埃及), 只有coin那那个花式还存在西班牙的牌桌上(oro).
|
|
新增了三个花式(它们的名字还有设计进行了几次更改).
|
|
然后意大利人将剑叫做锹.
|
|
得到一副传统的意大利扑克牌.
|
|
今天美国用的扑克牌是法国的变种, 修改了前两个花式:
|
|
还存在用于插入, 排序, 以及翻转列表的方法. 所有这些变动的操作都会修改列表的值; 它们不会创建一个新的列表对象.
共享和标识. 由于我们已经修改单个列表, 而不是创建一个新的列表, 因此对象绑定的名称chinese的值同样也会改变, 因为它跟suits绑定的是同一个列表对象.
|
|
这种行为是新的. 早先, 如果一个名称没有出现在一个语句中, 那么它的值就不会被这个语句影响到. 对于可变数据, 在一个名称上调用方法能够同时影响到其他的名称.
对于这里例子, 下面的运行环境图展示了跟chinese名称绑定的值是如何在只涉及到suits的语句中被修改的. 观察例子中的每一个步骤来查看这些改变.
列表对象可以用列表构造器函数来复制. 修改一个列表不会影响到另外一个, 除非它们共享相同的数据结构.
|
|
根据这种环境, 通过suits引用来修改列表会影响到nest的第一个元素的那个内嵌的列表, 但是不会对其他的元素有影响.
|
|
同样地, 在nest的第一个元素中撤销这个改动同样也会影响到suit
|
|
因为两个列表有可能会有相同的内容, 但是实际上是两个不同的列表, 我们需要一个手段来测试两个对象是否是相同的. Python含有两个比较操作符, 叫做 is 以及 is not, 用来测试两个表达式实际上是否得到的是相同的对象. 如果两个对象它们的当前值是一样的, 然后任何一个的改动都会反映到另一个对象中, 那么两个对象是相等的. 身份标识是比相等性更强的条件.
|
|
最后两个比照说明了 == 跟 is 两者的不同, 前者检查身份, 而后者则是检查内容的的相等性
列表推导. 一个列表推导总是会创建一个新的列表. 例如, unicodedata模块跟踪Unicode字母表中每一个字符的官方名称. 我们可以查找与名称相对应的字符, 包括那些扑克牌的花式.
|
|
这些结果列表并没有将它的内容跟suits进行共享, 执行列表表达式也不会改动到suits列表.
你可以在Dive into Python 3中的Unicode章节中, 查看更多相关的用于表示文本的Unicode标准.
元组
一个元组, 是一个內建的tuple类型的实例, 是一个不可变序列. 是用元组字面量, 也就是用逗号分割元素来创建的. 括号是可选的, 但是在实践中经常使用. 任何对象都可以放在元组中.
|
|
空的或者拥有一个元素的元组具有特殊的字面语法.
|
|
像列表, 元组具有有限的长度, 同时也支持元素选择. 它们同样也具有一些可用于列表的方法, 例如count以及index.
|
|
然而, 对于那些操作列表内容的方法在元组中是不可用的, 因为元组是不可变的.
因此无法改变元组中的元素, 但是可以修改一个包含在元组中的可变元素的值.
多重赋值中隐式地使用元组, 一个将两个值绑定到两个名称中的赋值语句会创建两个元素的元组然后对它进行解包.
2.4.3 字典
字典在Python中是一个內建的数据类型, 用来存储以及操作对应关系. 一个字典包含有多个键值对, 键跟值都是对象. 字典的目的是提供一个抽象化的用于存储以及检索数据并不以连续的整数而是描述性的键值为下标的地方.
通常用字符串来作为键值, 因为我们常用一个字符串名称来表示一样东西. 这个字典字面量给定各种罗马数字的值.
|
|
使用元素选择操作符通过它们的键来查看我们先前应用于序列的对应的值.
|
|
一个字典中每一个键最多只能有一个对应的值. 添加新的键值对或者通过键来修改已经存在的值都可以通过赋值语句实现.
|
|
注意到, L的值在前面的输出结果中是没有添加的. 字典是无序的键值对集合. 当我们输出一个字典, 键跟值会以某种顺序渲染, 而作为语言的用户, 我们无法预知将会按照何种顺序渲染. 当多次运行程序时这种顺序可能会改变.
字典也可以在环境图例中出现.
字典类型也支持多种用于迭代它包含的作为一个整体的字典内容的方法, keys, values以及items都返回一个可迭代的值
|
|
由键值对形式组成的列表可以通过调用dict构造函数来转化成一个字典.
|
|
字典也具有一些限制:
- 字典中的一个键不能对应多个值
- 对于一个给定的键最多只能有一个值.
第一个限制是跟Python字典底层实现相绑定的. 这个限制的细节不是本文的主题. 可以直观地认为键告诉Python在内存中哪里去找这个键值对; 如果这个key值改变了这个对的位置可能就会不见了. 元组通常也是可以在字典中作为键, 因为列表不可以用作键值.
第二个限制是字典抽象的一个必然结果, 那就是设计用一个键来存储以及检索一个值. 如果最多只有一个这样的值存在于字典当中, 我们只能用一个键来检索这个值.
一个由字典来执行的有用的方法是get, 这个方法要么会返回一个存在的键所对应的值, 要么返回一个默认值. 而get方法的参数就是键以及默认值.
|
|
字典也有一个类似于列表的解析式语法. 一个键表达式以及一个值表达式通过一个冒号隔开, 执行一个字典解析会创建一个新的字典对象.
|
|
2.4.4 本地状态
列表跟字典都有本地状态: 它们在程序运行的任意一个点上修改具有特定内容的值. “状态"这个词暗示了一个演变的过程, 表示这个状态可能会改变.
函数也可以具有本地状态. 例如, 让我们定义一个函数用于模拟从一个银行账户中提款的过程. 我们会创建一个叫做withdraw的函数, 它把一个数额作为它的参数. 如果这个账户具有足够的金额用于提款, 那么withdraw会返回提款后的剩余余额. 否则, withdraw会返回信息’资金不足’, 例如, 如果我们开始有$100在账户内, 我们会希望调用withdraw后能够得到下面的一系列的返回值
|
|
上面表达式withdraw(25), 运算了两次, 返回了不同的值. 因此, 这个用户定义函数是不纯的. 调用这个函数不仅返回一个值, 同时还会带有副作用以某种方式来改变这个函数, 因此下一次用相同的参数来调用函数会返回不同的值. 这个副作用是由withdraw函数更改当前环境的一个外部名称值的绑定而造成的.
为了让withdraw函数有意义, 它必须用一个具有余额的初始的账户来创建. 而函数make_withdraw是一个更高层次的函数, 需要一个初始余额作为参数. 而函数withdraw则是它的返回值.
|
|
make_withdraw的一个实现需要一种新类型的语句: 一个非本地的声明. 当我们调用make_withdraw时, 我们绑定名称balance到一个初始账户中. 然后我们定义并返回一个本地函数withdraw, 当调用这个函数时会更新以及返回balance的值.
|
|
nonlocal语句声明了无论任何时候我们改变名称balance的绑定值, 都会反映到这个balance第一个找到的绑定值的环境帧里面. 回想一下没有nonlocal声明, 一个赋值语句总是会绑定绑定一个名称到它的当前环境的第一个帧里面. 这个nonlocal语句表示名称出现在环境中除第一(本地)帧或最后(全局)帧之外的某处.
接下来的环境图例演示了多次调用make_withdraw创建的函数的影响.
第一个def语句具有通常的效果: 它创建了一个新的用户定义函数并在全局环境绑定名称make_withdraw到这个函数. 而随后调用make_withdraw创建并返回了一个本地定义的函数withdraw. 名称balance绑定在这个函数的父级帧中. 至关重要的是, 在该示例的其余部分中将仅存在用于名称balance的单个绑定.
接下来, 我们执行一个表达式来用金额为5的参数来调用这个绑定到名称wd上的函数. withdraw的函数体执行在新的拓展自withdraw被定义的的环境中. 跟踪函数withdraw的运行, 演示了nonlocal语句在Python中的效果: 一个在第一个局部帧外面的的名称能够通过赋值语句来修改.
nonlocal声明在withdraw的定义内修改所有剩余的赋值语句. 在执行nonlocal balance之后, 任何跟balance相关的把它放在等号左边的赋值语句都不会绑定balance到当前环境的第一帧里去. 相反, 它会找到balance已经被定义的第一个帧然后在这一帧内将把名称进行重新的绑定. 如果balance之前并没有跟一个值进行绑定, 那么nonlocal语句会抛出一个错误.
通过修改balance的绑定, 我们也修改了withdraw函数. 下一次它被调用时, 名称balance会执行15而不是20. 因此, 当我们第二次调用withdraw时, 我们会看到它返回值12而不是17. 第一次调用对balance的修改会反映到第二次调用的结果中去.
通常来说, 第二次调用withdraw会创建第二个本地帧. 然而, 两个withdraw帧具有相同的父级. 也就是说, 它们都拓展自那个包含有balance的绑定的make_withdraw的环境中. 因此, 它们共享那个特定的名称绑定. 调用withdraw函数具有改变环境的局部影响, 且会把这个影响延展到withdraw未来的调用中去. nonlocal声明允许withdraw函数来改变make_withdraw帧中的名称的绑定.
自从我们第一次遇到嵌套的def语句以来, 我们已经意识到本地定义函数可以访问它本地帧以外的名称. 访问非本地名称不需要nonlocal语句. 相比之下, 只有在nonlocal声明之后, 一个函数才能在这些帧里面修改名称的绑定.
通过介绍nonlocal声明, 我们已经为赋值语句创建了一个双重角色. 不管它们是修改本地绑定, 还是修改nonlocal绑定. 实际上, 赋值语句已经具有了双重性, 它们不仅可以创建新的绑定也可以重新绑定已经存在的名称. 赋值也可以修改列表以及字典的内容. Python中赋值中的许多角色会掩盖执行赋值语句的影响. 这取决于你作为一个程序员是如何文档化你的代码以清晰地表明赋值的影响来让其他人可以明白.
Python细节. 这种non-local模式的赋值是一个具有高阶函数以及词法作用域的编程语言的一般特性. 大部分其他的编程语言一点都不需要nonlocal声明. 反而, non-local赋值通常是赋值语句的默认行为.
Python对于名称的查找也具有一个不同寻常的限制: 在函数体内, 所有的名称的实例必须要指向同一帧. 因此, Python在一个non-local帧内不能查找到名称的值, 并绑定相同的名称到本地帧内, 因为相同的名称会在两个不同的帧内被同一个程序访问到. 这个限制允许Python在函数体执行前预先计算包含每个名称的帧. 当这个限制被违反时, 会产生混乱的错误结果信息. 作为演示, 下面重复make_withdraw示例, 并去除nonlocal语句.
出现了这个UnboundLocalError错误是因为balance在第五行被本地分配了一个本地值, 因此Python假设所有对balance的引用也必须出现在本地帧内. 这个错误出现在第五行被执行前, 意味着Python在执行第三行之前已经以某种方式考虑了第五行. 当我们学习解析器设计时, 我们会了解到在函数体执行之前进行预编译是相当普遍的事情. 在这个例子中, Python的预编译限制帧内可能出现balance, 因此预先阻止找到该名称. 添加一个nonlocal声明可以修复这个错误. nonlocal声明在Python 2中是不存在的.
非本地赋值的好处
非本地赋值在我们将程序看作是一个独立与自治的对象(也就是对象之间相互交互但各自管理他们自己内部的状态)的路上是重要的一步.
尤其是非本地赋值赋予了我们能力来管理一些函数的内部状态, 但是在调用这个函数时会发展出过度的连续性. balance与特定的withdraw函数相联系并共享于这函数的所有调用中. 然而为balance绑定到相联系的withdraw实例在程序的其余地方是不可访问的. 只有wd在它定义的make_withdraw帧内是可访问的. 如果make_withdraw再次被调用那么它会创建包含一个单独的balance绑定的一个单独的帧.
我们可以扩展我们的例子来演示这一点. 第二次调用make_withdraw返回第二个具有一个不同父级的withdraw函数.我们绑定这第二个函数到全局帧的名称wd2上.
现在我们可以看到那里其实有两个对balance的绑定在两个不同的帧里面,同时每一个withdraw函数都有一个不同的父级. 名称wd绑定到一个具有balance为20的函数上, 同时wd2绑定到一个具有balance为7的不同函数上.
调用wd2会修改它的非本地绑定名称balance, 但不会影响绑定到withdraw名称的函数. wd之后的调用不会受到wd2中改变的balance的影响, 它的balance依然是20
通过这种方式, 每一个withdraw的实例维护着它自己的balance状态, 但是这个状态对于程序中其他任何一个函数来说都是不可访问的. 在高层级来看这种情况, 我们已经创建了一个会管理它自己的内部但是以某种方式活动的生活中的账户模型的银行账户的抽象.
2.4.6 非本地赋值的成本
我们的计算环境模型清晰地拓展到解释非本地赋值的影响. 然而, 非本地赋值介绍了一些在我们思考名称以及值的方式上的重要的细微差别.
之前, 我们的值是不会修改的; 只有我们的名称以及绑定会修改, 当两个名称a以及b都绑定到一个值 4 上时, 它们是否绑定到相同的或者是不同的 4 是无所谓的, 据我们所知, 只有一个 4 对象且从不改变.
然而, 具有状态的函数不是以这种行为方式. 当两个名称 wd 以及 wd2 都绑定到一个withdraw函数上时, 对于它们是否绑定到同一个函数或者这个函数的不同实例上是有关系的. 考虑一下下面的例子, 它与我们刚刚分析的例子相对比. 在这种情况下, 调用命名为 wd2 的函数会修改命名为 wd 的函数的值, 因为这些名字都是引用同一个函数.
世界上用两个名称共同引用同一个值是很常见的, 所以它存在我们的程序当中. 但是, 值会随着时间而变化, 我们必须要小心理解对于修改其他名称而影响到这些名称会带来的结果.
正确地分析带有分本地赋值的代码的关键是要记住, 只有函数调用可以引入新的帧. 赋值语句总是在已存在的帧内修改绑定. 在这种情况下, 除非调用make_withdraw两次, 否则只能绑定一次balance.
相同和改变. 提出这些细微之处是因为随着会修改分本地环境的非纯函数的引入, 我们已经改变了表达式的性质. 一个表达式只包含纯函数调用的话是可靠透明的; 如果我们用其子表达式的值替换其子表达式之一, 它的值不会修改.
重新绑定操作符违反了透明引用这个条件因为它们除了返回一个值还做了更多的事情; 它们修改了环境. 当我们引入任意重绑定, 我们就遇到了一个棘手的认识论问题: 它意味着两个值是相等的. 在我们的计算环境模型中, 分别定义的两个函数不是相同的, 因为修改一个应该不会关联到另外一个.
一般来说, 只要我们从来没有修改数据对象, 我们可以认为复合数据对象恰好就是它所有部分的总和. 例如, 一个有理数取决于给定它一个分子和分母. 但是这种观点在存在变化的情况下已经不在有效, 也就是一个复合数据对象具有一个"身份标识”, 用来跟它组成的片段来进行区分的. 一个银行账户依然是"同一个"银行账户, 即使我们通过支取来修改了余额; 反过来, 我们可以有两个恰巧有相同余额的账户, 但是是两个不同的对象.
尽管它引入了复杂性, 非本地赋值依然是一个创建模块化程序的强力工具. 程序的不同部分对应着不同的环境帧, 能够随着软件的执行来分别演进. 此外, 使用带有本地状态的函数, 我们能够实现可变数据类型. 实际上, 我们可以实现相当于上面提到的內建的list以及dict类型的抽象数据类型.
2.4.7 列表以及字典的实现
Python语言并不允许我们访问列表的实现, 只是內建了序列抽象以及变动方法到语言里面去. 可以通过具有本地状态的函数来理解可变列表是如何进行表示的, 现在我们将会开发一个可变的链表实现.
我们会通过一个具有链表作为它的本地状态的函数来表现一个可变链表, 列表需要有一个身份, 就像其他任何可变值. 尤其是, 我们不能用 None 来代表一个空的可变列表, 因为两个空的列表不是相同的值(例如: 为其中一个列表插入元素并不会插入到另一个当中), 但是 None 就是 None. 另一方面, 两个都具有empty作为它的本地状态的不同的函数将足以用来区分两个空列表.
如果一个可变链表是一个函数, 它会需要什么传入什么参数呢? 答案展示了编程中的一般模式: 这个函数是一个调度函数同时它的参数首先是一个消息, 后面跟着参数化该方法的其他参数. 这个消息是一个字符串名称表示这个函数应该做什么. 调度函数实际上集合了许多的函数: 用消息确定函数的行为, 以及将额外的参数用在这个行为上.
我们的可变列表会回应5种不同的消息: len, getitem, push_first, pop_first, 以及str. 前两个实现序列抽象的行为. 接下来的两个用于增加或者移除列表的第一个元素. 最后一个消息返回代表整个链表的字符串.
|
|
我们也可以增加一个简便函数来从任何的內建序列中构造一个实现了功能的链表, 简单地相反的顺序来添加每一个元素.
|
|
在上面的定义中, 函数reversed接受并返回一个可迭代的值; 这是另一个函数处理序列的例子.
到现在, 我们可以构造一个实现了功能的可变链表. 要注意这个链表本身是一个函数.
|
|
此外, 我们可以输入信息到列表 s 来改变它的内容, 为实例移除它的第一个元素.
|
|
原则上, push_first以及pop_first足以对列表进行任意更改. 我们可以总是清空整个列表然后用期望的结果来替换它的旧内容.
消息传递. 给定一些时间, 我们可以实现很多Python列表的有用的变动操作. 例如extend以及insert. 对此我们可以进行选择: 我们可以使用已存在的消息pop_first以及push_first来进行所有的更改将它们都实现在一个函数里面. 或者, 我们可以添加额外的elif条件到dispatch函数体中, 每一个对一种消息进行检查(例如: extend)以及直接应用适当的修改到内容当中.
第二种方法, 就是将所有操作的逻辑封装到响应不同消息的一个函数内的数据值上, 这是一种称为消息传递的规则. 一个使用消息传递来定义调度函数的程序, 每一个这种函数都可以具有局部状态, 以及通过传递"消息"作为第一个参数来组织计算. 消息是对应特殊行为的字符串.
实现字典. 我们还可以实现一个具有跟字典类似行为的值. 在这种情况下, 我们用一个键值对的列表来保存字典的内容. 每个对是一个两个元素的列表.
|
|
再一次, 我们用消息传输方法来组织我们的实现. 我们已经支持两个消息: getitem和setitem. 为一个键插入一个值, 我们过滤出任何给定键的存在记录, 然后添加一个. 通过这种方式, 我们保证每一个键值在记录中只出现一次. 要为一个键找出它的值, 我们过滤出符合给定的键的值. 我们现在可以用我们的实现来保存以及检索值.
|
|
这种实现的字典没有为快速查找作优化, 因为每一次调用必须要过滤全部的记录. 內建的字典类型是十分高效的. 它的实现方式超出了本文的范围.
2.4.8 调度字典
调度函数是为抽象数据实现消息传递接口的一般方法. 为了实现消息调度, 迄今为止我们使用条件语句来对比消息字符串跟已知消息的固定集.
內建的字典数据类型提供一个一般的方法来查找一个键的值. 而不是使用条件来实现派发, 我们可以用字符串作为字典的键.
下面的可变account数据类型实现为一个字典. 它有一个构造器account以及一个选择器check_balance, 以及用于存储(deposit)或者取出(withdraw)资金的函数. 此外, 账户的本地状态也被保存在字典周围实现它的功能的函数中.
account构造器函数体内的dispatch到一个包含由帐户接受的消息作为键的字典进行绑定. 当存款以及取款消息绑定跟函数绑定, 余额就是一个数字. 这些函数能够访问dispatch字典, 同时, 它们也可以查看以及修改余额. 通过保存余额在dispatch字典中而不是直接保存在在account函数帧中, 我们避免了在deposit以及withdraw中需要用到nonlocal声明.
+=以及-=操作是Python(以及其他许多语言)中用于组合查找和重新分配的简便方法. 相当于下面的最后两行.
|
|
2.4.9 传播约束
可变数据允许我们去模拟具有改变的系统, 也允许我们去构建新类型的抽象. 在这个扩展例子中, 我们组合非本地声明, 列表, 以及字典来构建一个基础约束的系统, 它支持多种说明的计算. 作为约束的表达式程序是声明性编程的一种类型, 也就是一个程序员声明要去解决的问题的结构, 但是抽象出了究竟如何计算问题的解决方案的细节。.
计算机程序传统上是组织为单方向计算的, 也就是在预先指定的参数上执行操作来生产期望的输出. 另一方面, 我们通常想要以数量的关系来对系统建模. 例如, 我们以前思考过的理想气体定律, 它是通过玻尔兹曼常数(k)来跟压力(p), 体积(v), 数量(n), 以及温度(t)相关的.
p * v = n * k * t
这样的一个方程不是单项的. 有任意四个给定的数量, 我们可以用这个等式来计算第五个. 然而将这个等式转换到传统的计算机语言中或迫使我们去选择一个数量并用其他四个数量来计算出它. 因此, 一个计算压力的函数无法被用来计算温度, 即使所有需要计算的数量都源自同一个等式.
在本节中, 我们用线性关系来勾勒出一般模型的设计. 我们定义保留在数量之间的原始约束, 例如一个adder(a, b, c)约束会强制得到数学关系a + b = c.
我们还定义了一种组合方法, 因此原始约束可以被组合来表达出更多复杂的关系. 通过这种方式, 我们的程序就类似于一个程序语言. 我们通过构建一个由连接器连接来连接约束的网络来组合约束. 一个连接器是一个持有一个值以及并且可以参与一个或多个约束的对象.
例如, 我们知道华氏度以及摄氏度之间的关系是: 9 * c = 5 * (f - 32)
这个方程是c和f之间的复杂约束. 这样的一个约束能够想象为一个由原始adder, multiple以及constant约束组成的网络.
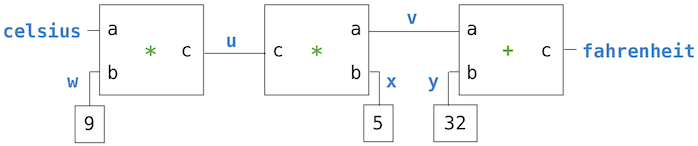
在这个图片中, 我们看到左边的乘法器有三个终端, 标记为a, b和c. 这些将乘法器连接到网络的其余部分, 如下所示: a终端是连接到一个连接器celsius, 它将会保存摄氏温度. b终端连接到一个连接器w中, 也就是一个连接到具有9的常量盒子的连接器. c终端是一个乘法器盒子约束为a和b的乘积, 连接到c终端的是另外一个乘法器, 这个乘法器的b终端连接到一个常量5而a终端连接到一个和约束的其中一项上.
这样的网络计算过程如下: 当一个连接器给定了一个值(通过用户或者它连接到的约束盒子), 它将会唤醒它所有关联的约束(除了那个唤醒它的约束)来通知它们它所具有的值. 每一次唤醒约束盒子然后轮询它的连接器来查看这里是否有足够的信息来确定一个连接器的值. 如果有, 这个盒子就设置这个连接器, 这个连接器随后会唤醒所有自己的关联约束等. 例如, 在摄氏度和华氏度之间的转换, w, x以及y都会立即被分别设置为常量盒子9, 5以及32. 连接器唤醒乘法器以及加法器, 它判断得出现在还没有足够的信息来继续执行. 如果用户(或者网络的其他部分)给celsius连接器设定一个值(比如说25), 那么最左边的乘法器会被唤醒, 然后它会设定u为25 * 9 = 225. 然后u会唤醒第二个乘法器, 它会设定v为45, 然后v唤醒加法器, 它会设置fahrenheit连接器为77.
使用约束系统. 要使用约束系统来执行上面描绘的温度计算, 我们首先通过调用connector构造器来创建两个已命名的连接器, celsius以及fahrenheit.
|
|
然后, 我们连接这些连接器到网络中来做一个上图的镜像实现. 函数convert用来装配网络中的各种连接器以及约束.
|
|
我们会用一个消息输入到系统中来协调约束以及连接器. 约束是不具有本地状态的一个字典. 约束不会直接修改连接器的值, 而是会通过发送信息来修改, 因此连接器可以通知其他的约束来响应修改. 通过这种方式, 一个连接器代表一个数字, 同时也封装连接器的行为.
一个我们可以发送到连接器的信息是设置它的值. 这里, 我们(也就是"用户”)设置celsius的值为25.
|
|
不仅仅celsius的值修改为25, 而且它的值通过网络传播, 因此fahrenheit的值也会修改. 这些值会被打印出来因为在构建它们的时候我们命名了这两个连接器.
现在我们可以尝试设定fahrenheit到一个新值, 比如说212.
|
|
这个连接器会抱怨说它探测到一个矛盾: 它的值是77.0, 然后某个人尝试将它设为212. 如果我们真的想要用新的值重用这个网络, 我们可以告诉celsius去忘记它的旧值:
|
|
连接器celsius发现那个本来要设定它值的用户现在正在撤回这个值, 因此celsius同意去丢掉自己的值, 然后它通知网络的剩余部分目前的情况. 这个信息最终传播到fahrenheit中, 它现在发现它没有理由去继续相信它拥有的值是77. 因此, 它也放弃了它自己的值.
现在, fahrenheit已经没有了值, 我们可以自由地设定它为212:
|
|
这个新值, 当其通过网络传播时, 迫使celsius得到一个值100. 我们已经使用这个非常相像的网络来通过给定fahrenheit计算celsius, 通过给定fahrenheit计算celsius. 这种计算的非方向性是基于约束的系统的区别特征。
实现约束系统. 就像我们看到的, 连接器是一个映射消息名称到函数以及数据值的字典. 我们会实现连接器来响应下面的消息:
connector['set_val'](source, value)表明source需要连接器来设置它的当前值为value.connector['has_val']()返回是否这个连接器已经具有一个值.connector['val']是connector的当前值.connector['forget'](source)告诉连接器需要它去忘记设定的source的值connector['connect'](source)告诉连接器去加入到一个新的约束中, 也就是source;
约束也是字典, 它会从连接器通过两个消息来接收信息:
constraints['new_val']()表明已经连接到约束并具有一个新的值的一些连接器.constraints['forget']()表明已经连接到约束并具有并忘记它的值的一些连接器.
当约束接收到这些信息, 它们恰当地将这些信息传播到其他的连接器.
adder函数通过三个连接器来构造了一个加法约束, 就是前两个必须要相加得到第三个: a + b = c. 要支持多向约束传播, 加法器也必须要能够指定从c减去a得到b以及同样的从c减去b得到a.
|
|
我们也愿意去实现一个通用的三元(三个方向)约束, 也就是用三个连接器以及三个函数从adder来创建一个约束来接受new_val以及forget信息. 响应消息的是被放置在一个字典中称为constraint的本地函数.
|
|
称为constraint的字典是一个调度字典, 但它本身也是一个约束对象. 它响应约束接收的两个信息, 但它在调用它的连接器时也作为source参数来传输.
无论任何时候约束被通知有一个它的连接器得到了一个值时, 约束的本地函数new_value就会被调用. 这个函数首先检查看是否a和b都有值. 如果有, 它会告诉c去设定值自己为函数ab的返回值, 在adder的情况下就是相加的结果. 约束将它自己(constraint)作为source参数来传输到connector中, 也就是adder对象. 如果a和b不是全都有值, 那么constraint会检查a以及c, 等等.
如果约束被通知到它的其中一个连接器已经忘记它的值, 它会要求它所有的连接器马上遗忘自己的值. (只有这些值是由约束设置的会真的丢失掉.)
一个乘法器跟一个加法器十分的相似.
|
|
一个常量也是一个约束, 但是一个永远不会发送任何信息的约束, 因为在它设置构建的时候只涉及到单一的一个连接器.
|
|
这三个约束足以实现我们的温度转换网络.
表示连接器. 一个连接器是作为一个包含一个值的字典来表示的, 但也有本地状态的响应函数. 这连接器必须跟踪给予其当前值的信息提供者以及它参与的约束的列表.
这个connector构造器有本地的函数来设置以及遗忘值, 它们是来自约束的消息的响应.
|
|
连接器再一次作为五个消息的调度字典用来通过约束去与连接器通信. 有四个是响应函数, 最后的一个是响应的值本身.
当有请求来设置连接器的值时本地函数set_value会被调用. 如果连接器当前不具有值, 它将设置其值并记住请求要设置的值的源约束为informant. 接着连接器会通知所有它参与的约束除了请求要设置值的约束. 这是使用以下的迭代函数完成的.
|
|
如果一个连接器被要求遗忘它的值, 它会调用本地的forget_value函数, 这函数首先检查确认请求最初设置的值是从相同的约束中来的. 如果是连接器通知它的关联约束关于值的丢失.
响应has_val消息指示出连接器是否有一个值. 响应connect消息会添加约束源到约束列表中.
我们已经设计好的约束程序介绍了许多思想将会在面向对象编程里面再次出现. 约束以及连接器都是通过消息操纵的抽象. 当连接器的值被修改, 它是通过消息改变的而且不仅仅改变值, 还验证它(检查源)以及传播它的影响(通知其他的约束). 实际上, 在这章之后, 我们会用一个相似的字典架构, 它包含字符串值作为键以及函数值来实现一个面向对象系统.
2.5 面向对象编程
面向对象编程(OOP)是一种组织程序的方法, 在这一章中它汇集并带来了许多思想. 比如在数据抽象中的函数, 类在数据使用和实现之间创建的抽象屏障. 比如调度字典, 对象回应行为请求, 比如可变数据结构, 具有本地状态的对象并不可以直接在全局环境访问. Python的对象系统提供了便利的语法来促进使用这些技术来组织程序. 许多这些语法都在其他的面向对象编程语言中共享.
对象系统提供的不仅仅是便利. 它为设计程序启用了新的隐喻, 也就是其中几个独立的代理在计算机中的交互. 每一个对象以提取两者复杂性的方式将局部状态以及行为捆绑在一起. 对象之间相互通信, 并且有用的结果从它们之间交互的成果中得出. 对象不仅仅传递消息, 它们也在相同类型的其他对象间共享行为以及在相关类型中继承特性
面向对象编程范例有它自己的词汇用来支持对象隐喻. 我们已经见识过一个对象就是一个具有方法以及属性通过点语法访问的数据值. 每一个对象都有一个类型, 叫做它的类. 要创建一个新的数据类型, 我们需要实现一个新的类.
2.5.1 对象以及类
一个类就是所有类型是这个类的对象的一个模板. 每个对象都是某种特定类型的类的一个实例. 到目前为止我们用过的所有对象都具有內建的类, 但是新的用户定义的类型也可以被创建. 一个类的定义指定了属性以及方法在这种类的对象之间共享. 我们会通过重看银行账户的例子来介绍类声明.
当介绍局部状态, 我们看到银行账户被自然地以具有balance的可变数据值来建模. 一个银行账户对象应该有一个withdraw方法来更新账户的余额以及在更新后的余额有效的情况下返回请求的金额. 要完成抽象, 一个银行账户应该可以返回它当前的余额(balance), 返回账户持有者(holder)的名称, 以及存款金额(deposit).
一个账户类允许我们去创建多个银行账户的实例. 创建一个新对象实例的动作被称为类的实例化. 在Python中实例化一个类的语法跟调用一个函数的语法是一样的. 在这种情况下, 我们用参数’Kirk’即账户持有者的名称来调用Account类.
|
|
一个对象的一个属性就是一个跟对象关联的名值对, 并且它能够通过点语法来访问. 特定对象的特定属性(与类的所有对象相对而言)称为实例属性. 每一个Account都有它的自己的余额以及账户持有者名称, 也就是例子的实例属性. 在更加广泛的编程社区, 实例属性也会叫做字段, 特性, 或者实例变量
|
|
在对象或者执行特定对象计算的函数被称为方法. 方法的返回值以及副作用可以取决于对象的其他属性且改变它. 例如, deposit(存款)是Account类对象a的一个方法. 它接收一个参数, 就是存款的金额, 修改对象的balance(余额)属性, 然后返回余额的结果.
|
|
我们称方法在特定的对象上被调用. 作为调用withdraw(取出)方法调用的结果, 要么取款会被批准并扣除总额, 要么请求被拒绝然后方法返回一个错误信息.
|
|
如上所述, 方法的行为可以取决于对象属性的修改. 对withdraw(取款)的两次相同的调用返回了不同的结果.
2.5.2 定义类
用户定义类型是通过包含一个单一条款的class声明来创建的, 一个class声明定义一个类的名称, 然后包含一系列语句来定义类的属性:
class <name>:
<suite>
当一个类声明被执行, 一个新的类就会创建并在当前环境的第一帧内绑定到<name>. 内部的一系列语句会执行. 任何在class声明的<suite>范围内的通过def或者赋值语句定义的名称会创建或修改类的属性.
类通常围绕操纵类的属性, 也就是跟这个类的每个实例相关联的名值对. 这个类通过定义用于初始化新对象的方法来指定其对象的实例属性. 例如, 初始化Account类的对象的其中一个部分是分配给它一个初始的余额值0.
类声明中的<suite>包含有def声明, 它会定义为这种类的对象定义新的方法. 在Python中初始化对象的方法具有一个特别的名字, __init__(在单词init的两边都有两个下划线), 这方法称为这个类的构造器.
|
|
Account类的__init__方法有两个形式参数. 第一个是self, 它绑定到的是最新创建的Account对象. 第二个参数是account_holder, 它在调用类来实例化对象的时候绑定为的传输给类的参数.
构造器将实例名为balance的属性绑定为值0. 它同时也将名为holder的属性绑定到名为account_holder具有的值. 形式参数account_holder在__init__方法中是本地名称. 另一方面, 最终通过赋值语句进行绑定的名称holder依然存在, 因为它通过点语法存储为self的属性.
在定义了Account类之后, 我们可以实例化它
|
|
这种"调用"Account类创建出来的新对象是Account的一个实例, 然后用两个参数: 最新创建的对象以及字符串Kirk来调用构造器函数__init__. 按照惯例, 我们用参数名self代表构造器的第一个参数, 因为它是绑定到已被实例化的对象上的. 这个惯例实际上在所有Python代码中被采用.
现在我们可以用点语法访问对象的balance以及holder.
|
|
身份. 每一个新的账户实例都有它自己的balance属性, 这个值独立于其他相同类型的对象.
|
|
为了强制这种分离, 每一个用户定义类的实例对象都有一个唯一的标识, 对象标识可以用is或者is not操作符来进行比较.
|
|
尽管都是从相同的调用中构造, 绑定到a的对象跟绑定到b的对象是不相同的. 而同样地, 用赋值语句绑定一个对象到新的名字不会创建新的对象.
|
|
新的用户定义类的对象只当一个类(例如Account)通过表达式语法调用进行实例化的时候才会被创建.
方法. 对象方法通常也通过类语句的套件内的def语句来定义. 下面, deposit以及withdraw都是作为Account类的方法来定义的.
|
|
虽然一个方法的定义跟一个函数的定义在如何声明上并没有什么不同, 但方法定义在它们执行的时候会带来不同的效果. 通过在class语句内部def语句创建的函数值会绑定到声明的名称上, 同时也会局部绑定作为类的属性. 这个值会从一个类的实例中通过点语法作为方法被调用.
每一个方法的定义再一次包含有特殊的第一参数self, 它是绑定到调用方法的对象上的. 例如, 我们会说deposit是在特定的Account对象上被调用的, 同时需要传单个参数值: 存款的金额. 对象本身被绑定到self上, 而参数绑定到amount上. 所有调用的方法都可以通过self参数访问对象, 同时, 它们全部都可以访问以及操纵对象的状态.
要调用这些方法, 我们再一次要用到点语法, 如下所示:
|
|
当一个方法通过点语法被调用, 对象本身(在这个例子中是绑定到spock_account上的对象)扮演一个双重角色. 第一, 它确定名称withdraw的含义; withdraw不是当前环境下的名称, 而是Account类的本地名称. 第二, 当withdraw方法被调用时它会绑定到第一个参数self.
2.5.3 消息传递与点表达式
那些定义在类里面的方法以及通常在构造器里面分配的实例属性, 都是面向对象编程的基本要素. 这两个概念在消息传递数据值的实现中复制了调度字典的大多数行为. 对象用点语法携带消息, 但那些消息不是任意字符串值作为键, 它们是作为类的局部名称而存在的. 对象也有命名的本地状态(实例属性), 但是这个状态可以使用点语法进行访问以及操纵, 而不用在实现中使用nonlocal语句.
消息传递的中心思想是数据值应该通过响应它们所代表的抽象类型的相关消息具有行为. 点符号是Python的一个句法特征, 用来形式化消息传递的隐喻. 使用具有內建对象系统的语言的好处是消息传递可以与语言的其他特性无缝互动, 例如赋值语句, 我们无需请求不同的消息来"获取(get)“或者"设置(set)“跟本地属性名称相关联的值; 语言的语法允许我们直接使用消息名称.
点表达式. 代码片段spock_account.deposit被称为点表达式. 一个点表达式由一个表达式, 一个点, 以及一个名称组成.
<expression>.<name>
<expression>可以是任意有效的Python表达式, 但是<name>必须是一个简单名称(不是一个运行后得到一个名称的表达式). 点表达式对<expression>的值代表的对象运算出给定的<name>属性的值.
內建函数getattr也通过一个名称返回一个对象的属性. 这是一个相当于点符号的函数. 使用getattr函数, 我们可以用字符串查看一个属性, 就像在调度字典中那样做.
|
|
我们也可以用hasattr测试一个对象是否具有某个属性.
|
|
对象的是属性包括所有的实例属性, 以及在其类中定义的所有属性(包括方法). 方法是类中需要特殊处理的属性
方法和函数. 当一个方法在一个对象上被调用, 对象会隐含地作为方法的第一个参数进行传输. 也就是说, 对象是点号左边的<expression>的值自动地作为第一个参数传输给点号表达式右边的方法名代表的函数. 结果就是对象绑定到参数self上.
要实现自动绑定self, Python将我们自本文开始以来一直创建的函数和绑定方法区分开来了, 这些方法将函数和要调用该方法的对象耦合在了一起. 绑定方法的值已经和它的第一个参数(也就是调用它的实例, 那个将在方法被调用时会命名为self的对象)关联在一起.
我们可以通过在交互式解析器上调用type来处理点语法的返回值来看出差异. 作为一个类的属性, 一个方法只是一个函数, 但是作为一个实例的属性, 它就是一个绑定了的方法:
|
|
这两个结果的不同事实上在于第一个是标准的带有两个形参self以及account的函数. 而第二个是具有单个形参的方法, 在方法被调用时名称self会被自动地绑定到名为spock_account的对象上, 而形参amount会被绑定到传入方法的参数上. 所有这些值, 无论是函数值或者绑定方法值, 都跟相同的deposit函数体相关联.
我们可以用两种方式调用deposit: 作为函数以及作为绑定方法. 在前一种情况下, 我们必须明确地提供一个参数给self形参, 在后一种情况下, self形参会自动绑定.
|
|
函数getattr的行为跟点符号完全类似: 如果它的第一个参数是一个对象, 但是名称是一个已经在类中定义的方法. 那么getattr返回一个绑定的方法值. 另一方面, 如果第一个参数是一个类, 那么getattr直接返回属性值, 也就是一个纯函数.
命名约定. 传统上命名类是使用CapWords惯例(也就是称为驼峰式, 因为在名称中间的单词首部看起来像是一个驼峰). 方法名跟随命名函数所使用的标准惯例也就是使用小写单词并用下划线作分割.
在某些情况下, 对象上跟维护性与一致性相关的一些实例变量以及方法我们是不希望对象的用户看到或者使用的. 它们不是类的抽象定义的一部分, 而是实现的一部分. Python的惯例规定如果一个属性名以下划线开始, 它就应该只能被类自身内部的方法访问到, 而不是使用这个类的用户.
2.5.4 类属性
一些属性值是共享给指定类的所有对象访问的. 这样的属性是跟类本身而不是任何个别类的实例相关联的. 例如, 让我们假设一个银行以固定利率支付账户余额的利息. 利率可能会变动, 但是这是一个在所有账户中共享的单一值.
类属性通过赋值语句在类的套件语句中且在所有方法定义的外面创建. 在更广泛的开发者社区中, 类属性可能也会叫做类变量或静态变量. 接下来的类语句中为Account类创建一个名为interest的属性.
|
|
这个属性依然可以从类的任何实例中访问到.
|
|
但是, 对类属性的单个赋值语句会更改该类的所有实例的属性值.
|
|
属性名. 我们已经在对象系统中引入了足够的复杂度, 以至于我们必须要指定如何将名称解析为特殊的属性. 毕竟, 我们可以轻易地拥有一个相同名称的类属性以及实例属性.
就像我们已经见识过的, 一个点表达式包含一个表达式, 一个点, 以及一个名称:
<expression>.<name>
去执行一个点表达式:
- 执行在点符号左边的
<expression>语句, 它返回的一个对象给点表达式. <name>跟对象的实例属性相匹配; 如果有一个这样名称的属性, 就会返回它的值.- 如果
<name>没有出现在实例属性之中, 那么会去类中查找<name>, (如果找到)并返回类属性的值. - 除非这个值是一个函数, 那么将会返回一个绑定了的方法. 否则属性值将被返回.
在执行过程当中, 实例属性的查找会在类属性之前, 就像本地名称对于全局环境名称所具有的优先权. 在类中定义的方法会跟点表达式中的对象结合通过执行第四步的过程形成一个绑定方法. 这个查找类中的名称的过程会有附加的细微差别, 一旦我们介绍类继承之后将会很快出现.
属性赋值. 在其左侧包含点表达式的所有赋值语句都会影响该点表达式对象的属性. 如果对象是一个实例, 那么赋值会设定一个实例属性. 如果对象是一个类, 那么赋值会设定一个类属性. 这个规则带来的后果是, 为一个对象赋值一个属性不能影响到它的类的属性. 下面的例子演示了这个区别.
如果我们为一个账户实例赋值一个名为interest的属性, 我们就创建了一个新的跟已经存在的类属性名称一样的实例属性.
>>> kirk_account.interest = 0.08
然后这个属性值会在点表达式中被返回
|
|
然而, 类属性interest仍然保留它的原始值, 提供给所有其他的账户返回.
|
|
更改类属性interest会影响到spock_account, 但是对kirk_account的实例属性不会有影响.
|
|
2.5.5 继承
当在面向对象模式下工作时,我们常常发现不同的类型是有关系的。尤其是,我们会发现相似类的在专有化程度上有所不同。两个类可能会有相同的属性,但是其中一个代表的是另一个的特殊例子。
例如,我们可能会想要实现一个支票账户,它跟标准账户有所不同。一个支票账户每次取钱都需要额外的$1手续费且具有更低的利率。这里,我们演示期望的行为。
|
|
一个CheckingAccount是一个专有化的Account。在OOP术语中,一般的账户会作为CheckingAccount的基类,而CheckingAccount会成为Account的子类(术语父类以及超类通常也用来表示基类,而子类通常也用来表示子集。)
一个子类继承它的基类的属性,但可能会重载某些属性,包括某些方法。有了继承,我们只需要指出子类与基类之间的不同。任何我们在子类中没有特别指明的都会自动假定它的行为跟基类一样。
继承除了是一个有用的组织性特性,在对象隐喻中也具有作用。继承代表的意思是类中"是一个"的关系,可与"有一个"的关系相类比。一个支票账户"是一个"特殊类型的账户,因此继承自Account的CheckingAccount账户就是继承的恰当使用。另一方面,一个银行"有一个"列的银行账户给它管理着,因此,都不应该继承其他,而是,账户对象列表会自然地表示为一个银行账户对象的实例属性。
2.5.6 使用继承
首先,我们给出Account的完整实现,包括类的文档字符串以及它的方法。
|
|
下面显示的是CheckingAccount的完整实现。我们通过在类名后的括号中放置一个运算后为基类的表达式来指定继承。
|
|
这里,我们引入一个在类CheckingAccount中指定的属性withdraw_charge。我们分配一个较低的值给interest属性。我们同样也定义一个新的withdraw方法来重新定义在Account类中的行为。在类中没有进一步的声明,所有其他的行为都是继承自基类Account。
|
|
表达式checking.deposit运算绑定的取款方法, 也就是定义在Account类内的方法. 当Python解析点表达式内不是实例属性的名称的时候, 它会在类内部查找名称. 实际上, 在类内"查找"的行为尝试去查找原始类继承链中的每个基类中的名称. 我们可以递归地定义这个过程. 来查找类中的名称.
- 如果它在一个类中命名了一个属性, 返回属性的值.
- 否则, 在基类中查找名称, 如果里面有一个的话.
在deposit的例子中, Python首先必定会在实例中查找名称, 然后在CheckingAccount类中查找. 最后会在Account类中查找, 也就是deposit定义的地方. 根据我们的点表达式运算规则, 由于deposit是在checking实例中查找类得到的函数, 即运算点表达式绑定方法的值. 此方法用参数10来调用, 会用绑定了checking对象的self以及绑定了10的amount调用deposit方法.
对象的类会一直保持不变. 即使deposit方法是在Account类中找到的, deposit调用时self绑定的实例还是属于CheckingAccount而不是Account.
调用祖先. 已经被重载的属性依然能够通过类对象来访问. 例如, 我们通过一个含有withdraw_charge的参数来调用Account的withdraw方法从而实现CheckingAccount类的withdraw方法.
注意到我们调用self.withdraw_charge而不是等价的CheckingAccount.withdraw_charge. 前者相对于后者的好处是一个继承自CheckingAccount的类可能会重写体现的手续费. 如果是这样的情况, 我们会想要让我们实现的withdraw找到的是新的值, 而不是旧的值.
接口. 在面向对象编程当中, 不同的类型的对象相互之间共享相同的属性名称是十分常见的. 一个对象接口是一个由属性以及建立在这些属性之上的条件的集合. 例如, 所有账户必须要有接受数值的deposit以及withdraw方法, 也有一个balance属性. 而类Account以及CheckingAccount都实现了这些接口. 在这种方式下继承尤其会促进命名共享. 在一些编程语言比如Java, 接口实现必须明确地被声明. 在其他如Python, Ruby以及Go中, 任何具有恰当名称的对象就是一个接口.
在你的程序中使用对象(而不是实现它们)的部分如果对于对象的类型没有作出任何假设, 而是只定义了它们的属性名称那么对于未来的修改这是最健壮的. 换句话说, 它们使用对象抽象而不是假设任何关于它的实现.
例如, 假如说我们运行一个彩票, 同时我们希望存入$5到账户列表的每一个账户中. 接下来的实现没有假设任何关于这些账户的类型, 因此, 能够在任何类型的具有deposit方法的对象下同等运行.
|
|
函数deposit_all只假设每一个account满足账户对象的抽象, 因此它会与任何其他也实现了这个接口的账户类工作. 假设一个特定的账户类会违反这个账户对象抽象的抽象屏障. 例如, 接下来的实现不一定能跟新类型的账户一起工作.
|
|
稍后, 我们将会在这一章详细讲述关于这个主题的更多细节.
2.5.7 多重继承
Python支持子类从多个基类中继承属性的概念, 这一语言特性被称为_多重继承_.
假设我们有一个继承自Account的SavingsAccount, 这个账户每次存款都会收取客户一点小费用.
|
|
然后, 一个聪明的执行官构思了一个AsSeenOnTVAccount账户, 它具有CheckingAccount以及SavingsAccount账户的最好的特性: 取款费用, 存款费用, 以及低利率. 这是集存款以及取款账户于一身的账户! 执行官的理由是: “如果我们构建它的话, 有人愿意建立账户并支付这些费用, 我们甚至会给他们一美元”.
|
|
实际上, 这个实现是复杂的. 分别使用定义在CheckingAccount以及SavingsAccount中的函数来取款以及存款都会产生费用.
|
|
无二义性引用能够按期望被处理:
|
|
但是当引用有歧义时会怎样呢, 例如在Account以及CheckingAccount都定义了的withdraw方法的引用? 下面的图例描绘了AsSeenOnTVAccount类的继承图. 每一个箭头都是从子类指向父类.
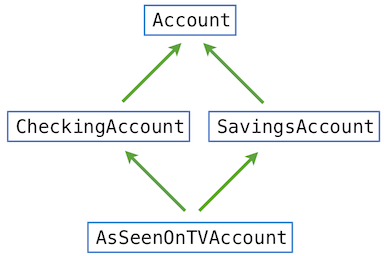
像这样一个的简单的菱形形状, Python是从左到右, 然后向上处理名称. 在这个例子中, Python按照以下类的排序来检查一个属性名称, 直到找到具有这样名称的属性:
AsSeenOnTVAccount, CheckingAccount, SavingsAccount, Account, object
这不是一个正确处理继承顺序问题的办法, 有一些例子中我们可能更倾向于给更高的优先级给某些继承的类而不是其他的. 然而, 任何支持多重继承的编程语言都必须要选择某些一致的顺序方式, 来让使用这个语言的用户可以预知他们的程序的行为.
进一步阅读. Python使用称作C3排序解决方法的递归算法来处理这个名称. 任何类方法的解决顺序可以在所有类中使用mro方法查询.
|
|
解决顺序的查找方法的精确算法不是本文的主题, 但是它被描述在Python的第一作者的原著论文的引用中.
2.5.8 对象的作用
Python对象系统是为了使数据抽象以及消息传递方便和灵活而设计的. 类, 方法, 继承, 以及点表达式的专有语法都是允许我们在程序中形象化对象的比喻, 也就是提升我们组织大型程序的能力.
特别地, 我们会希望我们的对象系统促进程序不同关注点的分离. 程序中的每个对象都封装并管理某部分的程序的状态, 同时每个类声明内定义的函数都实现了程序总体逻辑的一部分. 抽象屏障在大型程序的不同方面形成界限.
面向对象编程尤其适合去编写分离但是也有交互部分的模型系统. 例如, 不同用户在社交网络中交互, 不同的角色在游戏中交互, 以及不同的形状在物理仿真系统中交互. 当要表现这样的一个系统时, 在程序中的对象常常自然地映射到系统中已经建模的对象上, 同时类描绘它们的类型以及关系.
另一方面, 类可能不会提供最好的机制来实现某些抽象. 功能抽象为输入输出之间的关系表现提供更自然的隐喻. 不应该迫使在类中程序的每一点都符合逻辑, 尤其是当为了更自然地操作数据时定义的独立函数. 函数也可以实习分离关注点.
多范例语言如Python允许程序员对适当的问题来使用恰当的模式. 学习识别什么时候应该引入一个新的类, 或者与之对照的新函数为了简化或者模块化一个程序, 在软件工程中是一个重要的设计技能值得认真关注.
2.6 实现类以及对象
当在面向对象编程范式下工作时, 我们使用对象隐喻去指导我们程序的组织. 在类声明当中表达的大多数逻辑是关于如何表示以及操作数据的. 在这一节当中, 我们会看到类以及对象本身可以仅仅使用函数以及字典来表示. 用这种方法实现一个对象系统的目的是阐明用对象隐喻不需要特别的编程语言. Python可以是面向对象的, 甚至一个没有内建对象系统的编程语言也可以.
为了实现对象, 我们会抛弃点符号(需要内建的语言支持), 但是会创建一个调度字典, 它的行为跟内建的对象系统元素的大致一样. 我们已经见识过如何通过调度字典实现消息传递行为. 为了完全实现一个对象系统, 我们在实例, 类以及基类以及所有含有属性的字典当中发送消息.
我们不会实现整个Python对象系统, 其中包括在本文中没有覆盖到的特性(例如, 元类以及静态方法). 相反, 我们会专注于没有多继承也没有自省行为(例如返回一个类的实例)的用户定义类. 我们的实现并不意味着按照Python类型系统的精确规范. 相反, 这么做的目的是实现对象隐喻的核心功能.
2.6.1 实例
我们从实例开始. 一个实例具有命名的属性, 例如一个账户内的余额, 可以被设置以及恢复. 我们用一个调度字典实现一个可以响应"get"以及"set"属性值的实例. 属性本身被保存在一个叫做attributes的本地字典当中.
就像我们在之前的章节中看到的, 字典本身是抽象数据类型. 我们用列表实现一个字典, 我们用数据对来实现列表, 同时我们用函数来实现数据对. 当我们依据字典来实现一个对象系统时, 要记住的是我们也可以只用函数来实现对象.
要开始我们的实现, 我们假设我们有一个类的实现可以查找任何不是实例的一部分的名称. 我们进入一个传入参数cls的类make_instance当中.
|
|
instance是一个调度字典用来响应get以及set消息. set消息相当于Python的对象系统的属性赋值: 所有分配了的属性都直接保存在对象的本地属性字典当中. 在get方法中, 如果name不出现在本地的attributes字典中, 那么它会在类当中查找. 如果通过cls返回的value是一个函数, 它必须跟一个实例绑定.
绑定值方法. 在make_instance中的get_value函数通过类的get(方法)来找到一个命名属性, 然后调用bind_method方法. 绑定方法只用于函数值, 同时它通过插入实例作为第一个参数从一个函数值中创建一个绑定方法值.
|
|
当一个方法是可调用时, 通过这个定义第一个参数self会被绑定为值instance.
2.6.2 类
一个类也是一个对象, 都存在于Python的对象系统以及现在我们这里实现的系统. 为了简单起见, 我们的类并没有它们自己的类型. (在Python中, 类都是有它们自己的类型的; 几乎所有的类都共享相同的类型, 叫做type.) 一个类可以响应get以及set消息, 也可以响应new消息:
|
|
不像一个实例, 当找不到一个属性的时候类型的get函数不会查询它的类, 取而代之的是查询它的基类. 类不需要进行方法绑定.
初始化. 在make_class的new函数调用init_instance, 首先会创建一个新的实例, 然后调用叫做__init__的方法.
|
|
这最后的函数完成了我们的对象系统. 我们现在有会在局部set但是get时可回退到它们的类的实例. 一个实例在它的类中查找名称之后, 它绑定它自己本身到一个函数值来创建一个方法. 最后, 类可以创建新(new)实例, 然后它们在实例创建之后立即应用它们的__init__构造器函数.
在这个对象系统, 唯一应该通过用户调用的函数是make_class. 所有其他的功能通过消息传递来激活. 同样地, Python的对象系统是通过class声明来调用, 以及所有它的其他功能通过点语法以及调用类来激活.
2.6.3 使用已经实现的对象
我们现在回到之前章节的使用银行账户的例子. 使用我们实现了的对象系统, 我们会创建一个Account类, 一个CheckingAccount子类, 以及一个各自的实例.
Account类是通过make_account_class函数创建的, 也就是跟在Python中的class声明有相似结构的函数, 但是以调用make_class结束.
|
|
最后调用locals返回一个有字符串为键的字典, 它在局部帧中包含新的名值绑定.
Account类最后是通过赋值来实例化的.
|
|
然后, 一个账户实例通过new消息来创建, 也就是需要一个名称来给新创建的账户.
|
|
然后, get消息传递给kirk_account来检索属性以及方法. 方法可以被调用来更新账户的余额.
|
|
就像Python的对象系统, 设置一个实例的属性不会修改它对应的类的属性.
|
|
继承. 我们可以通过重载一个类的属性的子集来创建一个子类CheckingAccount. 在这个例子中, 我们修改withdraw方法去征收费用, 同时我们降低利率.
|
|
在这个实现中, 我们从子类的withdraw函数调用基类Account的withdraw函数, 就像在Python的内建对象系统中一样. 我们可以像之前一样创建子类本身以及一个实例.
|
|
存款的行为完全相同, 跟构造函数一样. 取款从特殊的withdraw方法征收$1的费用, 同时interest有来自于CheckingAccount的新的更低的值.
|
|
我们的建立在字典之上的对象系统跟Python内建的对象系统的实现是十分类似的. 在Python中, 任何一个用户定义类的实例都具有一个特别的属性__dict__用于在字典中为这个对象存储本地实例属性. 就像我们的字典attributes. Python的不同在于它区分某些跟内建函数交互的特别方法以确保这些函数行为对很多不同类型的参数是正确的. 在不同类型上操作的函数是下一节的主题.
2.7 对象抽象
对象系统允许程序员去高效地建立以及使用抽象数据表示. 它同样也设计为允许在同一程序内共存多重数据抽象表示.
对象抽象的一个中心概念是泛型函数, 也就是一个可以接受多种不同类型值的函数, 在实现泛型函数中我们会考虑三种不同的技术: 共享实例, 类型派发, 以及强制类型. 在建立这些概念的过程中, 我们也会发现Python的对象系统中的特性也就是支持泛型的创建.
2.7.1 字符串转换
为了有效地表示数据, 一个对象值应该表现得像它所代表的类型的数据, 包括产出它自身所代表的字符串. 数据值的字符串表示在交互式语言中是十分重要的, 例如Python会自动地展示交互式会话中的表达式的值的字符串表示.
字符串值提供了在人之间进行传达信息的基本介质. 字符序列可以被渲染到屏幕上, 打印到纸上, 大声读, 转换成盲文, 或者以摩尔斯密码广播. 字符串同样也是编程的根本因为它们可以表示Python的表达式.
Python规定所有的对象应该产出两种不同的字符串表示: 一种是可以被人类解释的文本以及一种是可以被Python解释的表达式. 字符串的构造函数str, 返回一个可以被人类阅读的字符串. 在可能的情况下, repr函数返回一个Python表达式, 其运算结果为相等的对象. repr的文档字符串解释了这个属性:
repr(object) -> string
返回对象表示的标准字符串.
对大多数对象类型来说, eval(repr(object)) == object.
对一个表达式的值调用repr的结果就是Python打印在交互式回话中所打印的.
|
|
在原始值没有表达存在的情况下, Python通常会产出一个被角括号包围的描述.
|
|
str构造器通常跟repr重合, 但是在某些情况下会提供更多的可解释文本的表示. 例如, 我们会看到在dates对象上str与repr之间的不同.
|
|
定义repr函数提出了一个新的挑战: 我们想要它在所有类型的日期下都能够正确应用, 即使这些类型在repr实现的时候还不存在. 我们会想要让它成为一个通用或者多态性函数, 一个可以被应用在很多(聚合/poly)不同类型(变形/morph)的数据.
在这种情况下, 对象系统提供一个优雅的解决办法: repr函数总是调用它参数上的一个叫做__repr__的方法.
|
|
通过在用户定义类上实现这一相同的方法, 我们可以拓展repr的适用性到未来我们创建的任何类上. 总的来说, 这一例子强调了点表达式的其他好处, 就是它们提供了将现有函数的域扩展为新对象类型的机制.
str构造器也是以相似的方式实现: 它调用参数上的一个叫做__str__的方法.
|
|
这些多态函数用于演示更一般的原理: 某些函数应该应用到多种数据类型上. 此外, 创建此类函数的一种方式是在每个类上使用不同定义的共享属性名称.
2.7.2 特殊方法
在Python中, 某些特殊方法是通过Python解析器在特殊情况下调用的. 例如, 无论什么时候一个对象被创建时类的__init__方法会自动被调用. 当进行打印时__str__会自动被调用, 以及__repr__在互动式回话中被调用来显示值.
Python中有许多其他行为的特殊名称. 其中一些最常使用的已经描述在下面.
真假值. 前面我们看到在Python中数字具有真实值; 更进一步来说, 0代表假值而其他所有数字代表真值. 实际上, 在Python中的所有对象具有真值. 默认地, 用户定义的类的对象都认为是真值, 但是特殊方法__bool__可以用来重载这个行为. 如果一个对象定义了__bool__方法, 那么Python将调用这个方法来判断它的真实值.
举个例子, 假设我们想要让一个余额为0的银行账户是假值. 我们可以添加一个__bool__方法到Account类来创造这个行为.
|
|
我们可以调用布尔构造器来查看一个对象的真实值, 然后我们可以使用布尔上下文中的任何对象.
|
|
序列操作. 我们已经知道可以使用len函数来确定序列的长度.
|
|
len函数调用它的参数的__len__方法来判断参数的长度. 所有內建序列类型都实现这一方法.
|
|
如果一个序列没有提供__bool__方法, Python会使用一个序列的长度来判断它的真实值. 空序列为假值, 而非空序列则为真值.
|
|
__getitem__方法通过元素选择操作符来调用, 但它也可以被直接调用.
|
|
可调用对象. 在Python, 函数是一等对象, 因此它们可以作为数据进行传递以及可以像其他对象一样具有属性值. Python也允许我们通过引入一个__call__方法来定义一个像函数一样可以"调用"的对象. 使用这种方法, 我们可以定义一个行为像高阶函数的类.
举个例子, 考虑下接下来的高阶函数, 它会返回一个函数这个函数会添加一个常量值到它的参数上.
|
|
我们可以创建一个定义了__call__方法并提供相同功能的Adder类.
|
|
这里, Adder类的行为跟高阶函数make_adder相似, add_three_obj对象的行为跟add_three函数的行为相似. 我们进一步地模糊了数据与函数之间的界限.
算术. 特殊方法还可以定义应用于用户定义对象的内置运算符的行为. 为了提供这种一般性, Python遵循特殊协议来应用每一个操作符. 例如, 要运行含有+操作符的表达式, Python检查特殊方法表达式左右两边的操作数. 首先, Python检查左操作数的__add__方法的值, 然后检查右操作数的__radd__方法的值. 如果任意一个能找到, 这个方法会以其他操作数的值作为参数被调用. 一些例子将在下面的章节中给出. 对于想要进一步了解细节的读者, Python文档描述了完整的操作符名称集. Dive into Python 3 也有一个特殊方法名称集章节, 它描述了有多少这些特殊方法名称被使用.
2.7.3 多重表示
抽象屏障允许我们分离数据的使用以及表示. 然而, 在大型程序中, 对程序中的数据类型表示为"底层表示"并不总是有意义的. 一方面, 对数据对象可能有多个有用的表示, 同时我们可能喜欢去设计可以处理多重表示的系统
举个简单的例子, 复数可能会用两种相等的方式来表示: 以直角坐标形式(实部和虚部)以及以极坐标形式(幅度和角度). 有时候直角坐标形式更加适合, 而有时候极坐标形式更加适合. 实际上, 考虑这样的一个需要表示两种形式的复数系统以及能在其中一种表示下操纵复数来工作的函数是十分合理的. 我们会在下面实现这样的一个系统. 作为附注, 我们正在开发一个系统, 它会对复数执行算术运算来作为使用通用操作的程序的简单但不现实的例子. 复数类型在Python中是內建类型, 但对于这个例子我们会实现自己的复数类型.
允许数据进行多重表示的想法常常会出现. 大型软件系统通常由许多长期工作的人设计, 且受制于随时间变化的要求. 在这样的环境下, 允许为每个人提前选择好数据的表示是根本不可能的. 此外, 数据抽象屏障从使用中隔离了表示, 我们需要隔离彼此不同的设计选择的抽象屏障并允许不同设计选择在单个程序中共存.
我们会在高层次的抽象以及朝实现具体表示上来设计自己的实现. 一个Complex是一个Number, 而数字可以加或者乘在一起. 抽象了的数字如何能够通过名为add以及mul的方法被加或者乘在一起.
|
|
这个类要求数字对象具有add以及mul方法, 但是没有定义它们. 它甚至没有提供一个__init__方法. Number的目的不是用来直接实例化, 而是作为超类为各种指定数字类型提供服务. 我们的下一个任务是定义适合于复数的add以及mul方法.
一个复数可以想象成是由两个正交轴形成的二维空间中的一个点, 实轴以及虚轴. 从这个角度看, 复数c = real + imag * i(这里的i * i = -1)可以认为是一个平面上的点, 它的水平坐标是real, 垂直坐标是imag. 复数加法涉及到增加它们各自的real轴以及imag轴的坐标.
当乘以复数时, 将其想象成一个极坐标上以幅度和角度表示的复数会更加自然. 两个复数的乘积的结果就是的到一个向量值, 由其中一个复数的向量值跟另一个复数的向量值长度因子的乘积的得到, 然后加上一个角度值, 由其中一个复数的角度, 旋转值为另一个向量的角度得到.
Complex类继承自Number类, 并描述了复数的算术.
|
|
这个实现假设对于复数存在两个类, 跟复数的两个自然表示相对应:
ComplexRI从实部和虚部来构造一个复数ComplexMA从向量和角度来构造一个复数
接口. 对象属性是消息传递的一种形式, 允许不同数据类型以不同的方式来响应相同的消息. 从不同类中引出相同行为的一组共享消息是一种强大的抽象方法. 一个_接口_就是一个共享属性名以及它们的行为规范的集合. 在复数的例子中, 接口需要实现由四个属性组成的算法: real, imag, magnitude和angle.
想要在复杂的算术上是正确的, 这些属性必须要一致. 也就是说, 直角坐标系(real, imag)以及极坐标系(magnitude, angle)必须在复平面上是描述相同的点. Complex类通过决定这些属性如何用于跟一个复数来进行add以及mul从而隐式定义这个接口.
属性. 要求两个或多个属性值保持彼此之间的固定关系是一个新的问题. 一个解决办法是只为其中一个表示保存属性值然后其他表示则在它们需要的时候计算出来.
Python具有一个简单功能用于从零参数函数即时计算属性. @property装饰器允许调用函数而不调用表达式语法(跟随表达式后的括号). ComplexRI类保存real以及imag属性, 同时一经请求则计算magnitude和angle.
|
|
这个实现的结果是, 全部的四个复数算法需要的属性都可以不用任何调用表达式就访问到, 同时修改real以及imag都会反映到magnitude以及angle中.
|
|
同样地, ComplexMA类保存magnitude以及angle, 但当real以及imag被查找时会立马计算得出.
|
|
修改magnitude或者angle都会立马反映到real以及imag属性上.
|
|
我们现在已经完成了复数的实现. 实现了复数的任意类可以在任意Complex的算法上使用任意的参数.
|
|
编码多个表示的借口方法具有吸引人的属性. 类可以为每个表示单独开发; 它们必须也只需商定共享的属性的名称, 以及这些属性的任何行为条件. 接口是额外附加的. 如果其他程序员想要添加第三个复数的表示到相同的程序中, 它们只需要创建另外一个具有相同属性的类.
数据的多重表示跟我们这章的一开始的数据抽象的思想密切相关. 使用数据抽象, 我们能够去修改数据类型的实现而不修改程序的含义. 通过接口以及消息传递, 我们可以在相同的程序内有多种不同的表示. 这两种情况下, 名称集合以及对应的行为条件定义了实现这种灵活性的抽象.
2.7.4 通用函数
通用函数是一个可应用在不同类型参数上的方法或者函数. 我们已经见识过很多的例子. Complex.add方法是通用的, 因为它采用ComplexRI或者ComplexMA作为other的值. 这个灵活性是通过确保ComplexRI以及ComplexMA的共享同一个接口来获得的. 使用接口以及消息传递只是一些用来实现通用函数的方法其中的一种. 在这一节中, 我们会考虑其他两个: 类型调度以及类型强制.
假设, 除了我们的复数类型, 我们实现了一个Rational类来代表准确的分数. add以及mul方法跟本章之前的add_rational以及mul_rational表示相同的计算.
|
|
我们通过给超类包含add记忆mul方法已经实现了接口. 结果是, 我们可以用熟悉的操作来加上以及相乘有理数.
|
|
然而, 我们还是不能将一个有理数加到一个复数上, 即使在数学上已经明确定义了这样的组合. 我们想要以一些小心控制的方式来介绍这种跨类型操作, 因此我们可以假设它没有严重违反我们的抽象屏障. 这跟我们所期望的结果之前存在紧密的关系: 我们想要能够将一个复数添加到一个有理数上, 以及我们想要一般方法__add__能够对所有的数字类型都做正确的事情. 同时, 为了维护程序的模块化, 我们想要尽可能分离复数与有理数的关注.
类型调度. 一种实现跨类型操作的方式是基于函数或方法的参数的类型来选择行为. 类型调度的思想是去写一个函数来检查它们接收的参数的类型, 然后为这些类型执行合适的代码.
內建函数isinstance接受一个对象以及一个类. 如果对象所具有的类是这个类或者是继承自这个类的话就返回真值.
|
|
类型派发的一个简单的例子是一个为不同类型的复数使用不同的实现的is_real函数.
|
|
类型派发并不总是使用isinstance来执行的. 对于算术, 我们会为字符类型的Rational以及Complex的实例提供一个type_tag属性, 这个属性是一个字符串值. 当两个值x以及y都具有type_tag, 那么我们就可以用x.add(y)直接合并它们. 如果没有, 我们需要一个跨类型操作.
|
|
要将复数跟有理数结合, 我们需要编写同时依赖它们表现类型的函数. 接下来, 我们依赖一个事实, 那就是一个Rational可以近似转换为一个实数的float类型值. 这个结果可以用复数来进行组合.
|
|
乘法涉及到相似的转换, 在极坐标下, 在复平面上的实数总是具有一个正的向量. 角度0表示一个正数, 角度pi表示一个负数.
|
|
乘法跟加法都是可交换的, 因此交换参数顺序可以用这些跨类型操作的相同实现.
|
|
类型调度扮演的角色是去确保这些跨类型操作在适当的时候使用. 下面, 我们重写Number超类为其__add__以及__mul__来使用类型调度.
我们使用type_tag属性来区分参数的类型. 也可以直接使用內建的isinstance方法, 但是tags简化了实现. 使用类型标签也表明了类型调度不需要跟Python的类型系统相链接, 而是用于在异构域上创建通用函数的一般技术.
__add__方法考虑两种情况. 首先, 如果两个参数具有相同的类型的标签, 那么它假设第一个参数的add方法可以以第二个参数作为它的参数. 否则, 它检查是否一个跨类型的字典实现, 叫做adders, 包含一个可以对具有这些类型标签的参数进行相加的函数. 如果有这样的一个函数, cross_apply方法并应用它. __mul__方法具有相似的结构.
|
|
在新的Number类中, 所有跨类型实现都通过一对类型标签标记在adders以及multipliers字典中.
这种基于字典的类型调度方法是可拓展的. 新的Number子类型可以通过声明一个类型标签以及添加跨类型操作到Number.adders以及Number.multipliers从而安装到系统中. 它们也可以定义在子类中定义自己的adders以及multipliers.
虽然我们引入了一些复杂性到系统中, 但我们现在可以混合类型在加法以及乘法表达式中.
|
|
强制转换. 一般情况下完全不相关的操作作用于完全无关的类型上, 实现明确的跨类型操作也许是可以期望的最好的方式, 虽然它可能会很麻烦. 幸运的是, 有时我们可以通过利用在我们的系统中潜在的附加结构来做得更好. 不同的数据类型通常是不完全独立的, 并且这里或许存在将一种类型的对象看做是另外一种类型对象的方式. 这过程叫做强制转换. 例如, 如果我们被要求以算术将有理数和复数进行结合, 我们可以将有理数看作是复数且它的虚部是0. 这样做了之后, 我们可以用Complex.add以及Complex.mul来结合它们.
一般情况下, 我们可以通过设计强制转换函数实现这个想法, 这个函数可以转换一种类型的对象到另一种类型的等量对象. 这里是一个典型的强制转换函数, 它可以转换一个有理数为一个虚部是0的复数:
|
|
Number类的替代定义通过尝试强制转换两个参数为相同的类型来执行跨类型操作. coercions字典通过类型标签元组对索引所有可能的强制类型, 指示相对应的值将所述第一种类型的值强制转换为第二种类型的值.
通常不可能每种数据类型的任意数据对象强制转换成其他所有类型. 例如, 没有办法将强制转换一个任意复数为有理数, 因此没有这样的强制转换实现会出现在coercions字典中.
coerce方法返回两个具有相同类型标签的值. 它检查它的参数的类型标签的值, 将它们跟coercions字典的条目对比, 然后用coerce_to转换一个参数类型为另一个参数的类型. 在coercions中只需要一个条目来完成我们的跨类型算术系统, 并替换类型调度版本的Number中的四个跨类型函数.
|
|
这个强制类型方案跟定义显示跨类型操作的方法相比有一些优点. 虽然我们还是需要编写强制转换函数来关联类型, 但我们只需要为每一对类型编写一个函数, 而不是为每个类型集合以及每个通用操作使用不同的函数. 我们在这里期望要指出的事实是, 类型之间的适当转换仅依赖于类型本身, 而不是以来要应用的特定操作.
更进一步的好处来自于扩展强制转换. 一些更复杂的强制转换方案并不是仅仅是尝试去强制转换一种类型到另一种, 而是可能会尝试去强制转换每个不同的类型到第三种常见类型. 考虑一个菱形以及一个矩形: 两者都不是彼此类型的额外情况, 但是都可以被看作是四边形. 另一个强制转换的扩展是强制转换迭代, 一种数据类型通过中间类型被强制转换成另一种类型. 思考一下一个整数可以被转换成一个实数只要首先将它转换成一个有理数, 然后将这个有理数转换成实数. 以这种方式的链接强制转换可以减少程序所需的强制函数的总数.
尽管强制转换具有好处, 但也有潜在的缺点. 一个是强制函数在应用它们时可能会丢失信息. 在我们的例子中, 有理数是精确表示, 但是当它们被转换成复数时就成了近似值.
一些编程语言有內建自动的强制转换系统. 实际上, 早期版本的Python有一个__coerce__特殊方法在对象上. 最后, 内置强制系统的复杂性没有证明它的使用是有理的, 因此它被移除了. 而是, 特定运算根据需要对它们的参数应用强制转换.
2.8 效率
决定如何表示以及传输数据常常收可供选择的效率影响. 效率指的是表示或处理过程使用的计算资源, 例如函数计算结果或者表示一个对象需要用到多少时间以及内存. 这些数量根据实现的细节可以有很大的差异.
2.8.1 测量效率
精确地测量一个程序需要多长时间来运行或者消耗多少内存是一个挑战, 因为结果取决于很多电脑配置的细节. 一个更可靠的方式去描绘程序效率特征的方式是去测量某些事件发生了多少次, 例如函数的调用.
让我们回到第一个数递归函数, fib函数用于计算斐波那契数列中的数字.
|
|
思考一下下面描述的来自于计算fib(6)的结果的计算模式. 去计算fib(5), 我们需要计算fib(3)以及fib(4). 要计算fib(3), 我们需要计算fib(1)以及fib(2). 一般来说, 演进的过程看起来像一棵树. 每个蓝色点表示一个完整的计算斐波那契数的这棵树的遍历.
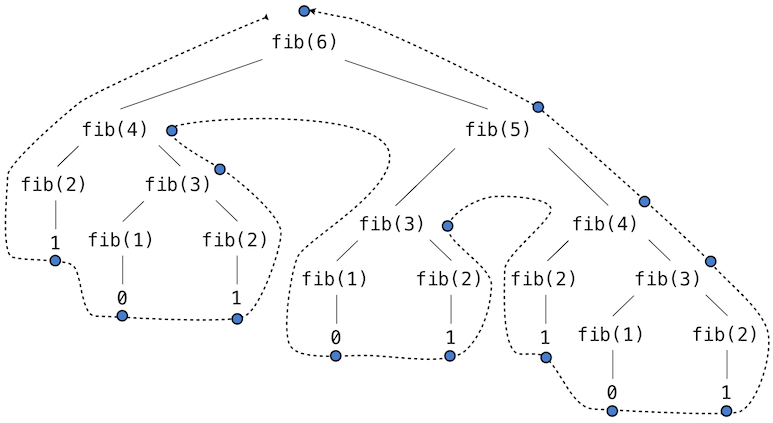
这棵树是典型的用于指导树递归的例子, 但是这是一个非常没有效率的计算斐波那契数的方式, 因为它做了许多冗余的计算. fib(3)的整个计算过程是多余的.
我们可以测量这种低效率. 高等级的count函数返回一个跟它的参数(也维持一个call_count属性)的等效函数. 用这种方法, 我们可以检查fib调用了多少次.
|
|
通过统计调用fib的次数, 我们可以看到需要的调用次数增长得比斐波那契数字本身要快很多. 这种快速增长的调用次数就是树递归函数的特征.
|
|
空间. 要明白函数对空间的要求, 我们必须要指出在我们的计算环境模型中一般会有多少空间被使用, 保存以及回收. 在计算表达式时, 解析器保存所有的活动环境以及被这些环境所引用的所有的值和帧. 一个环境如果它需要为某些需要将要运行的表达式提供执行上下文那么它就是活动的. 任何时候当创建函数调用的第一个帧最后返回的时候, 这个环境就变为非活动状态.
例如, 当计算fib, 解析器按照前面展示的顺序对每个值进行计算, 遍历树结构. 这样做, 只需要在计算树中的任何节点时对当前节点的上一个节点保持跟踪. 用于执行剩下的分支的内存是可回收的, 因为它不能影响到未来的计算. 一般来说, 树递归函数需要的空间跟树的最大深度成正比.
下面的图例描绘了执行fib(3)时创建的环境. 在执行最初的fib程序的返回的表达式的过程中, 表达式fib(n-2)被运行, 产生值0. 一旦这个值计算完成, 相应的环境帧(灰色淡出的那个)就不再需要了: 它不再是活动环境的一部分. 因此, 一个设计良好的解析器可以回收用于存储这个帧的内存. 另一方面, 如果这个解析器当前正在执行fib(n-1), 那么一个环境会通过fib程序(在这里的n是2)创建且是活动的. 反过来, 原来创建的应用3的fib环境依然是活动的, 因为它的返回值还没有被计算出来.
高阶的count_frames函数追踪open_count函数, 调用函数函数f的次数依然没有返回. max_count属性是通过open_count而获得的最大值, 而且它跟在计算过程中同时处于活动状态的帧的最大数相对应.
|
|
总的来说, 在活动帧中测量的fib函数需要的空间小于输入, 其趋势是趋向更小的. 在总的递归调用中测量的时间需求是大于输出的, 其趋势是趋向更大的.
2.8.2 记忆化
树递归计算过程通常可以通过记忆化技术来提高效率, 一个强有力的提高递归函数重复计算的效率的技术. 一个记忆化函数会对之前收到的任何参数的返回值进行存储. 第二次调用fib(25)不会再次递归计算返回值, 而是返回已经被构造而存在的那个值.
记忆化可以很自然地以高阶函数来表示, 也可以作为一个装饰器来使用. 下面的定义为之前的计算结果创建一个cache, 并以计算它们的参数作为索引. 字典的使用需要传给记忆化函数的参数是不可变的.
|
|
如果我们应用memo到斐波那契数的递归计算当中, 就演变出一种新的计算模式, 如下所示.
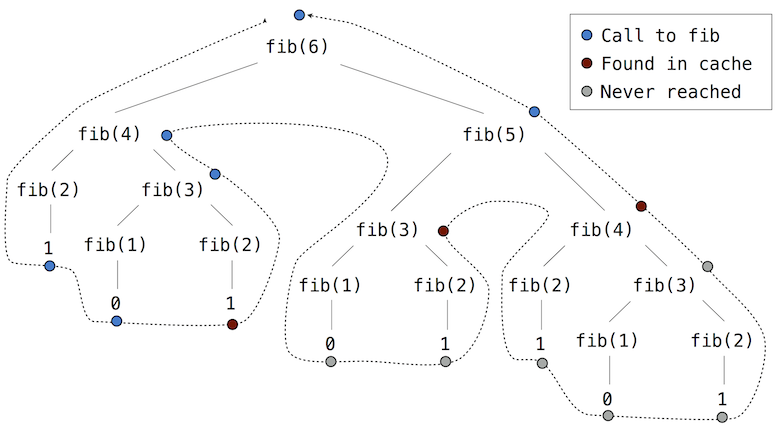
在fib(5)的计算当中, 在树右侧的分支上fib(2)以及fib(3)的计算结果在计算fib(4)时被重用. 结果就是, 树递归的许多计算结果是不必要的.
使用count, 我们可以看到fib函数实际上只对于fib的每个唯一输入调用一次.
|
|
2.8.3 增长的顺序
进程在消耗计算机时间以及空间资源上可以有巨大的不同, 就像先前的例子演示的那样. 然而, 当调用函数时精准地确定多少空间或时间会被使用是非常困难的任务, 这依赖于很多因素. 一个分析进程的有用的方式是将其分类为一组具有类似需求的进程组. 有效的分类是以进程的_增长顺序_来进行, 简单来说就是进程的资源需求随着函数的输入而如何增长.
作为增长的顺序的介绍, 我们会在下面分析函数count_factors, 它会统计可以将输入均分的整数的个数. 这个函数会尝试去把n跟每个小于或者等于它的平方根的数进行相除. 这个实现利用如果k可以整除n同时k < 根号n, 那么就有另一个因子j = n / k, 这样的j > 根号n这一事实.
执行count_factors需要多少时间? 精确的回答会随着机器的不同而变化, 但是我们可以做一些有用的涉及到计算量的一般性观察. 这个进程执行内部的while语句主体的总次数是小于根号n的最大整数. 在while语句之前或者之后的语句都只执行一次. 因此, 总的执行语句的次数是w * 根号n + v, 这里的w是指在while体内的语句的数量, 而v是指在while语句外面的语句. 虽然这样并不精确, 这个公式通常能够表明执行以n为输入的count_factors函数需要多少时间.
一个更加准确的描述是很难实现的. 常量w以及v并不是真正的常量, 因为赋值语句有时候会对因子执行有时候不会. 增长的顺序分析允许我们去掩饰这些细节从而分析增长的总体形态. 尤其是, count_factors增长的顺序精确地表示为一个术语, 那就是计算count_factors需要的时间量与根号n等比例缩放, 外加一些常量因数.
Theta符号. 让n成为一个参数用来衡量输入到某些过程的大小, 同时让$R(n)$成为输入大小为n的过程所需要用到的资源的总数. 在我们之前的例子中, 我们让n作为我们的给定的函数需要去计算的数字, 但也有其他的可能性. 例如, 如果我们的目标是去计算一个数字的平方根的近似值, 我们可能会取n为所需精度的位数.
$R(n)$可能会测量所需要使用的内存, 执行的基本机器步骤的数量等等. 在计算机中每一步只用固定的时间来执行, 运行表达式所用的时间将与在运行过程中执行的基本机器步骤的数量成比例.
我们说$R(n)$增长的顺序为$R(n)$, 写作$R(n) = \Theta(f(n))$ (读作"theta f(n)"), 如果有正的常数k1以及k2独立于n像下面这样:
$$
\begin{equation*}
k_1 \cdot f(n) \leq R(n) \leq k_2 \cdot f(n)
\end{equation*}
$$
对于任何大于某个最小值m的值n. 换句话说, 对于大n, 值$R(n)$总是夹在两个以$f(n)$为规模增长的区间当中:
- 一个下限$k_1 \cdot f(n)$以及
- 一个上限$k_2 \cdot f(n)$
我们可以用应用这个定义来展示运行count_factors(n)所需要的步骤数, 通过检查函数可知其增长为$\Theta(\sqrt{n})$.
首先, 我们选择$k_1=1$以及$m=0$, 使得count_factors(n)的下限状态为对于给定的$n>0$需要执行至少$1 \cdot\sqrt{n}$步. 这里至少有4行是在while声明之外执行的, 每一行至少需要一个步骤来执行. 这里至少有两行是在while体内执行的, 包括while头部本身. 所有这些至少需要一个步骤. while体至少执行$\sqrt{n}-1$次. 将这些下限进行合并, 我们可以看到, 过程至少需要$4 + 3\cdot (\sqrt{n}-1)$步, 也就是总是大于$k_1 \cdot\sqrt{n}$.
其次, 我们可以确认上限. 我们假设在count_factors体内的任何单一的一行最多需要p个步骤. 这个假设对于Python中的每一行都不是真的, 但可以适用于这种情况. 然后, 执行count_factors(n)至多需要$p \cdot(5 + 4 \sqrt{n})$步, 因为这里有5行在while声明之外, 以及4行(包括头部)在while之内. 这个上限能够保证即使if头部执行为真的情况也适用. 最后, 如果我们选择$k_2=5p$, 那么需要的步骤总是小于$k_2 \cdot \sqrt{n}$. 我们的论点是完整的.
2.8.4 例子: 指数
思考一下计算一个给定数字的指数的问题. 我们会想要一个函数来接受一个基础值b以及一个正整数的指数n然后计算$b^n$. 一个解决方式是通过一个递归定义来实现.
$$
\begin{align*}
b^n &= b \cdot b^{n-1} \
b^0 &= 1
\end{align*}
$$
这很容易转换成为递归函数
|
|
这是一个线性递归过程, 需要$\Theta(n)$部以及$\Theta(n)$的空间. 正如阶乘一样, 我们可以容易地制定一个相等的线性迭代函数, 它需要相似数量的步数, 但只需要固定的空间.
|
|
我们可以通过连续平方以更少的步数来计算指数. 例如, 不是这样计算$b^8$:
$$
\begin{equation*}
b \cdot (b \cdot (b \cdot (b \cdot (b \cdot (b \cdot (b \cdot b))))))
\end{equation*}
$$
我们可以用三个乘法来计算它:
$$
\begin{align*}
b^2 &= b \cdot b \
b^4 &= b^2 \cdot b^2 \
b^8 &= b^4 \cdot b^4
\end{align*}
$$
这个方法在指数是2的倍数的时候可以很好地工作. 一般来说, 如果我们使用递归规则, 我们也可以在计算指数上利用连续平方.
$$
\begin{equation*}
b^n = \begin{cases} (b^{\frac{1}{2} n})^2 & \text{if $n$ is even} \
b \cdot b^{n-1} & \text{if $n$ is odd}
\end{cases}
\end{equation*}
$$
我们也可以以一个递归函数来表示这个方法:
|
|
演化为fast_exp的过程其空间以及步数都以n的对数的规模来增长. 为了看到这一点, 观察用fast_exp计算$b^{2n}$只需要比$b^n$多计算一个乘法. 因此, 我们可以计算的指数的大小被允许是每个新的乘法的翻倍(大约). 由此, 乘法的次数需要一个指数n, 这乘法的次数的增长跟以2为底数的n的对数增长得一样快. 这过程增长为$\Theta(\log n)$. $\Theta(\log n)$增长与$\Theta(n)$增长的不同随着n的增大而变得明显. 例如, fast_exp对于n为1000的情况只需要14次乘法而不是1000次.
2.8.5 增长类别
增长顺序的设计旨在计算简化计算过程的分析以及比较. 很多不同的计算过程都可以具有相同的增长顺序, 这表示它们规模增长的方式是相似的. 计算机科学家必须知道并识别常见的增长顺序以及鉴别具有相同顺序的过程.
常量. 常量并不会影响过程的增长顺序. 因此, 例如, $\Theta(n)$以及$\Theta(500 \cdot n)$具有相同的增长顺序. 这个属性遵循theta符号的定义, 也就是允许我们去为上下限选择任意常量$k_1$以及$k_2$(例如$\frac{1}{500}$). 为了简单起见, 常量在增长序列中总是被省去的.
对数. 对数的基数并不会影响增长顺序的过程, 例如, $\log_2 n$以及$\log_{10} n具有相同的增长顺序. 修改对数的基数等于乘以常数因子.
嵌套. 当一个内部计算过程在外部计算过程的每一步中都重复(执行), 那么整个过程的增长的顺序就是内部和外部过程的中的步骤数的乘积.
例如, 下面的函数overlap计算共同存在于列表a以及列表b中的元素的个数.
|
|
in操作符对于列表而言需要$\Theta(n)$的运行时间, 这里的n是列表b的长度. 它出现了$\Theta(m)$次, 这里的m指的是列表a的长度. 表达式item in b是一个内部的过程, 而表达式for item in a循环是外部过程. 这个函数的总的增长顺序是$\Theta(m \cdot n)$.
低阶项. 随着对过程输入的增长, 计算中增长最快的部分主宰着总的资源的消耗. Theta符号能捕捉这种直觉. 总的来说, 除了增长最快的部分, 其他部分都可以抛弃掉而不会对增长的顺序有什么影响.
例如, 考虑一下one_more函数, 它会返回列表a中有多少个元素是比a中的其中一个元素多一的情况. 也就是说, 列表[3, 14, 15, 9], 元素15比14多一, 因此one_more会返回1.
|
|
这个计算有两个部分: 列表解析以及调用overlap. 对于长度为n的列表a, 列表解析式需要$\Theta(n)$个步骤, 而调用overlap需要$\Theta(n^2)$个步骤. 总的步数是$\Theta(n + n^2)$, 但这不是表达增长顺序的最简单的方法.
$\Theta(n^2 + k \cdot n)$以及$\Theta(n^2)$对于任意的常量k都是相等的, 因为$n^2$项对任何k最终都会支配总量. 事实上建立这种等价性边界必须要保持n大于某个最小值m. 为了简单起见, 低阶项总是在增长顺序中舍去, 因此我们永远不会在一个theta表达式中看到总和.
常见类别. 给定这种等价性, 出现了一小组常见类别的集合用于描述大多数常见的计算过程. 最常见的已经按照最慢的增长到最快的增长顺序列举在下面, 以及随着输入的增长而增长的描述. 下面是每个类别的例子.
| Category | Theta Notation | Growth Description | Example |
|---|---|---|---|
| Constant | $\Theta(1)$ | Growth is independent of the input | abs |
| Logarithmic | $\Theta(\log{n})$ | Multiplying input increments resources | fast_exp |
| Linear | $\Theta(n)$ | Incrementing input increments resources | exp |
| Quadratic | $\Theta(n^2)$ | Incrementing input adds n resources | one_more |
| Exponential | $\Theta(b^n)$ | Incrementing input multiplies resources | fib |
也存在其他的类别, 例如count_factors的增长$\Theta(\sqrt{n})$. 这些类别也是特别常见的.
指数增长描述了许多不同的增长顺序, 因为修改基数b会影响增长的顺序. 例如, 我们的树递归斐波那契计算函数fib的步数随着它的输入n以指数级增长. 特别地, 可以证明第n个斐波那契数是最接近下面等式的整数:
$$
\begin{equation*}
\frac{\phi^{n-2}}{\sqrt{5}}
\end{equation*}
$$
这里的$\phi$是黄金分割比率:
$$
\begin{equation*}
\phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180
\end{equation*}
$$
我们还指出所需的步骤数与结果成比例, 因此树递归过程需要$\Theta(\phi^n)$个步骤, 这是随着n指增长的函数.
2.9 递归对象
对象可以具有其他对象来作为属性值, 当某个类的对象具有一个属性值, 这个属性值也属于相同的类, 那么这就是一个递归对象.
2.9.1 链接列表类
链接列表, 在之前的章节里面介绍过, 由一个元素以及列表其余的部分组成. 列表的其余部分本身也是一个链接列表 – 一个递归定义. 空列表是链表中的一个特殊的情况, 它没有第一个元素以及其他元素. 一个链表是一个序列: 它具有有限的长度以及支持通过索引来选择元素.
现在我们可以实现一个具有相同行为的类. 在这个版本中, 我们会使用特殊方法名来定义它的行为从而允许我们的类能跟內建的len函数以及在Python中的元素选择操作符(方括号或者operator.getitem)工作. 这些內建函数调用类中的特殊方法名: 长度是通过__len__来计算的, 同时, 元素选择是通过__getitem__来计算的. 空链表是通过一个空的元组来表示, 也就是具有的长度是0同时没有元素.
|
|
__len__以及__getitem__的定义事实上是递归的. 当以用户定义的对象作为参数应用到內建的Python函数len上时会调用一个叫做__len__的方法. 同样的还有元素选择操作符会调用叫做__getitem__的方法. 因此, 这两种方法的主体内会间接地调用它们自己. 对于__len__, 当self.rest等于一个空的元组时就到达基本情况了, 也就是Link.empty具有的长度为0.
內建的isinstance函数返回第一个参数是否是第二个参数的类型或者继承自第二个参数的判断结果. 如果rest是一个Link的实例或者是一个Link子类的实例, 那么isinstance(rest, Link)的结果就是真值.
我们的实现已经完成了, 但是目前却很难检查一个实例是不是Link类. 为了有助于调试, 我们也可以定义一个函数来将Link转换成一个字符串表达式.
|
|
这种展现Link列表的方式是如此的方便以至于我们想要在任何时候都使用它来展现Link的实例. 我们可以通过设定link_expression函数作为特殊的类属性__repr__的的值来确保这个行为. Python通过调用实例的__repr__方法来展现用户定义类的实例.
|
|
Link类具有闭合属性. 就像一个列表中的元素本身可以是一个列表, 一个Link可以包含一个Link作为它的第一个元素.
|
|
s_first链接列表室友两个元素, 而它的第一个元素是一个包含三个元素的链接列表.
|
|
递归函数尤其适合用来操作链表. 例如, 递归函数extend_link函数构建了一个包含一个Link类的实例s紧跟着另一个Link类的实例t的元素的链表. 将这个函数作为__add__方法安装到Link类来模拟内部列表的添加行为.
|
|
除了列表表达式, 可以使用两个高阶函数来从一个链表生成另一个链表: map_link以及filter_link函数. 下面定义的map_link函数应用一个函数f到链表s的每个元素上同时构造一个链表来包含结果.
|
|
filter_link函数返回一个包含所有链表s中经f函数处理并返回真值的元素的链表. map_link以及filter_link的组合可以表达与列表表达式相同的逻辑.
|
|
join_link函数递归构造一个字符串, 它包含链表元素并以某些separator字符串来分隔开. 结果比link_expression的输出更加紧凑.
|
|
递归构造. 当需要递增地构造序列的时候链表尤其有用. 这在递归计算中经常会出现这种情况.
第一章的count_partitions函数通过树递归过程统计用最大递增到m的整数来划分整数n的方法的总数. 使用序列, 我们也可以用类似的过程来显式地枚举这些区间.
我们按照与计数时相同的逻辑来递归分析这些问题: 使用最大递增为m的整数划分整数n涉及下面两者之一:
- 区间
n-m使用最大递增到m的整数, 或者 - 区间
n使用最大递增到m-1的整数
对于最基本的情况, 我们发现0具有空的划分, 当划分一个负整数或者使用小于1的部分是不可能的.
|
|
在递归的情况下, 我们构造了两个分区子列表. 第一个使用m, 同时我们添加m到来自于with_m的结果using_m的每一个元素中.
partitions的结果是高度嵌套的: 链表的链表. 通过用恰当的分割符来使用join_link, 我们可以以人类可读的方式来显示分区.
|
|
2.9.2 树类
树也可以用用户定义的类来表示, 而不是嵌套內建的序列类型的实例. 一棵树可以是任何的数据类型, 它具有一个同样也是树的属性来作为的分支.
内部值. 之前, 我们以这样的方式来定义树, 那就是所有值都出现在树的叶子节点中. 这也是通常用来定义每个子树的根节点具有内部值的树的常见方法. 一个内部值在树内被称为entry. 下面的Tree类展示了这样的一棵树, 其中每棵树具有一个序列分支, 这个分支同样也是树.
|
|
树类可以进行表示, 例如, 在表达式树中表达fib这个计算斐波那契数的函数递归实现的计算值, 下面的fib_tree(n)函数返回一个Tree, 这个值具有第n个斐波那契数作为它的entry属性的值以及在其分支内保持一个对先前所有计算的斐波那契数的跟踪.
|
|
以这种方式表示的树也是用递归函数来处理的. 例如, 我们可以合计树的条目. 最基本的情况, 我们会返回一个空的没有条目的分支.
|
|
我们也可以应用memo来构造一个斐波那契树, 这个树中重复的子树只会通过记忆化版本的fib_tree创建一遍, 但是会被不同的更大的树多次使用.
|
|
在这些情况下, 通过记忆保存的计算时间和存储器的量是相当大的. 不是创建18,454,929个Tree类型的实例, 我们现在只需要创建35个.
2.9.3 集合
除了列表, 元组以及字典, Python还有第四种內建容器类型叫做set(集合). 集合字面量遵循的数学符号是用大括号包裹元素. 重复的元素将会在构造时被移除. 集合是一个无序集, 因此打印出来的顺序可能与集合字面量中设置的顺序不同.
|
|
Python集合支持各种操作, 包括成员测试, 长度计算, 以及取交集和并集这样的标准集合操作.
|
|
除了并集以及交集, Python集合还支持几个其他的方法. 断言isdisjoint, issubset以及issuperset提供集合比较(能力). 集合是可变的, 可以通过add, remove以及pop一次修改一个元素. 其余的方法提供多元素改动, 例如clear以及update. 在课程讲述的这个点上, Python的集合文档应该足够用来理解并填充细节了.
实现集合. 抽象地, 一个集合是一个不同对象的集, 它支持成员测试, 并集, 交集, 以及附加. 附加一个元素同时集合会返回一个新的集合, 这个新集合包含所有的原来集合的元素以及新的元素, 前提是这些新的元素不同于原来集合的元素的话. 并集和交集返回一个集合包含的元素是分别出现在任一集合或者两个集合都出现的元素. 与任何数据抽象一样, 我们可以自由地在任意集合的表示之上实现任何函数来提供这个集合的行为.
在这一节剩下的内容当中, 我们考虑三种不同的方法来实现一个集合的不同的表现形式. 我们会通过分析集合操作增长的顺序来描述这些不同表示的效率. 我们会使用到来自于本章前面部分的Link以及Tree类型, 这些类型允许实现简单而且优雅的递归解决方案用于初级的集合操作.
集合作为无序序列. 一种表示集合的方式是作为一个没有元素出现多于一次的序列. 空集合是通过空序列表示. 成员测试则是以递归的方式遍历列表.
|
|
这个set_contains的实现平均需要$\Theta(n)$的时间来测试成员是否包含元素, 这里的n是指集合s的大小. 对包含的成员使用这个线性时间的函数, 我们可以连接一个元素到集合中, 这个操作也是线性的.
|
|
在设计表示时, 一个我们需要考虑到的问题是效率. 对两个集合set1以及set2进行取交集也需要用到成员测试, 但是这一次, 每一个在set1中的元素必须在set2中进行成员测试, 这导致指令的增长为步数的二次方, $\Theta(n^2)$, n是两个集合的大小.
|
|
当计算两个集合的并集, 我们必须要小心不要去包含任何元素两次. union_set函数也需要线性次数的隶属测试, 创建一个过程也包含$\Theta(n^2)$个步骤.
|
|
集合作为有序序列. 一个提高我们集合操作的方式是修改表示以便让集合元素以递增的顺序列出. 要做到这个, 我们需要一些方法来比较两个对象以便于让我们可以说出那个更大. 在Python, 很多不同类型的对象可以用<以及>来进行比较, 但是在这个例子中我们会集中在数字上. 我们会通过递增的方式来列出它的元素来通过一个数字表示一个集合.
按顺序的一个好处出现在set_contains里面: 在检查一个对象是否出现上, 我们不用再去扫描整个集合. 如果我们拿到一个集合的元素, 它大于我们需要的元素, 那么我们就知道元素不在这个集合中:
|
|
这样的做法节省了多少步骤呢? 在最糟糕的情况下, 我们查找的项可能是在集合中最大的那项, 因此步骤数跟无序表示方式用的步骤数一样. 另一方面, 如果我们查找的项有很多不同的大小我们可以预期有时我们能够在列表的开始之初就停止搜索, 而其他时间我们还是需要检查列表的大部分. 平均来说, 我们可以预期需要检查结合中的半数. 因此, 平均需要的步数会近乎$\frac{n}{2}$. 这依然是$\Theta(n)$级增长, 但是它在实践中比以前的实现节省了我们一些时间.
我们可以通过重新实现intersect_set来取得更好的速度上的提升. 在无序表示中, 这个操作需要$\Theta(n^2)$个步骤, 因为我们的实现是为set1的每个元素来对set2进行完全扫描. 但是在有序表示中, 我们可以用一个更加聪明的办法. 我们同时迭代两个集合, 跟踪在set1中的元素e1以及set2中的元素e2. 当e1和e2相等时, 我们将这个元素囊括在交集中.
然而假设, e1比e2小. 因为e2比set2中的剩下的元素都要小, 我们可以立马得出结论e1不可能出现在set2中剩余的任何元素中, 因此, 它就不会在交集中出现. 由此, 我们就不需要再考虑e1; 我们丢弃它并开始处理下一个set1的元素. 也可以用相似的逻辑来处理set2当e2 < e1时. 这里是函数实现:
|
|
去预估这个过程所需的步骤, 可以观察到在每一步中我们至少缩小集合一个元素的大小. 因此, 需要的步数最多就是set1以及set2加起来的总和, 而不是像无序表示那样结果为两个集合大小的乘积. 这是$\Theta(n)$的增长速度而不是$\Theta(n^2)$的增长速度, 甚至对中等大小的集合而言, 这也是一个可观的速度提升. 例如, 取两个大小为100的集合的交集会需要200步, 而不是无序表示的10,000步.
以有序序列表示的集合的连接和联合也可以用线性时间计算出来. 这些实现就留作练习用.
以搜索树表示的集合. 我们比有序表示做得更好, 通过排列集合元素形成一个只具有两个分支的树中. 树的根节点entry持有一个集合的元素. 这个条目中左边的分支内包含所有小于根节点的元素. 右边的分支包含所有大于在根节点的元素. 下面的图像展示了一些树用来表示结合{1, 3, 5, 7, 9, 11}. 相同的集合可能会通过树以多种不同的方式来表示. 在所有的二叉搜索树中, 所有在左边的元素必须小于根节点的条目, 而所有在右边的子树必须比根节点条目大.

树表示的好处有这些: 假设我们想要检查一个值v是否包含在集合中, 我们通过比较v与进入点entry开始. 如果v是比它小的话, 我们就知道我们只需要搜索左边的子树; 如果v是比它大的话, 我们只需要搜索右边的子树. 现在, 如果这个树是"均衡的”, 每一个这些子树会大约是原始尺寸的一半. 那么, 在一个步骤中, 我们就已经将搜索大小为n的树的问题减少为搜索大小为$\frac{n}{2}$的问题. 因此树的大小在每一步都缩减一半, 我们应该可以遇见需要去搜索树的步骤数增长为$\Theta(\log n)$. 对于大型的集合, 这将会比前面的表示有更加显著的加速. 这个set_contains函数采用树结构集的排序结构.
|
|
链接一个项到集合中的实现也是类似的, 同时它需要的步数也是$\Theta(\log n)$. 去链接一个值v, 我们将v与entry进行比较来判断v是否应该添加到左边或者右边的分支上, 以及链接v到恰当的分支后, 我们将这些新的构造分支跟原始的entry项以及其他分支拼凑在一起. 如果v等于入口entry项, 我们就只是返回节点就可以了. 如果我们被要求链接v到一个空的树, 我们就构造一个具有v并以其作为entry入口的左右分支为空的Tree. 这里是它的函数实现:
|
|
我们声称搜索这些树可以以对数的步骤数来执行是基于树是"均衡的"这一个假设, 即每棵树的左以及右子树具有大约相同的数量的元素, 因此每棵子树包含有它的父级的一半的元素. 但是现在我们可以确定我们构造的树会是均衡的吗? 即使我们由一个均衡的子树开始, 通过adjoin_set添加元素后也可能会产出一个不均衡的结果. 因为新链接的元素的位置取决于元素是如何与已经存在集合中的项目进行比较, 我们可以预期如果我们添加元素是"随机的”, 那么平均来说, 树会趋于均衡.
但并不能够保证一定是这样的. 例如, 如果我们开始于一个空的集合, 然后按顺序链接1到7到集合中, 我们最终会得到一个高度不均衡的树, 它的所有左子树都是空的, 因此它相比于简单的顺序列表没有任何优势, 一个解决办法是去定义一个操作来转换一个任意的树为具有相同的元素的一个平衡树. 我们可以在每几个adjoin_set操作之后执行这个转换来保持集合的平衡.
交集和并集操作可以以线性时间在树结构的集合上执行, 通过转换它们为有序列表然后转换回来. 细节实现就留作练习.
Python集合实现. set类型是內建在Python中且没有在内部使用任何这些表示. 相反地, Python使用一个表示, 查找以及链接操作只需要恒定时间执行, 其实现基于一个被称为_哈希_的技术, 而这是另外的一个课程的主题. 內建Python集合不能包含可变数据类型, 例如, 列表, 字典, 或者其他集合. 为了允许集合嵌套, Python也包含了一个內建的不可变frozenset类, 它共享set类型的方法, 除了可变方法以及操作.